Přednášky        Zadání teoretických otázek a úkolů Řešení teoretických otázek a úkolů Vzorové řešené příklady Příklady na procvičení

1

1.1

1.2

1.3

1.4

1.5

1.6

1.7

1.7.1

1.7.2

1.7.3 Přímka a rovina

Přímka  je rovnoběžná s rovinou  právě tehdy, jestliže směrový vektor  přímky a normálový vektor  roviny jsou k sobě kolmé.

Úhel přímky s rovinou určíme jako doplňkový k úhlu, který svírají směrový vektor  přímky a normálový vektor  roviny: .

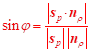Přímka jako průsečnice dvou rovin. Směrový vektor  přímky  vypočítáme jako vektorový součin normálových vektorů a  rovin  a : . Bod  ležící na přímce  určíme jako libovolný společný bod obou rovin ze soustavy dvou obecných rovnic rovin  a , a to soustavy s jedním volitelným parametrem.

Příklad

Sestavte parametrické rovnice přímky, která je průsečnicí roviny  a roviny .