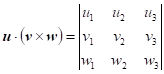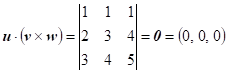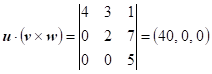Přednášky Zadání teoretických otázek a úkolů Řešení teoretických otázek a úkolů Vzorové řešené příklady Příklady na procvičení

1

1.1

1.2

1.3

1.4

1.5

1.6

1.6.1

1.6.2

1.6.3

1.6.4 Smíšený součin

Č.	Otázky	Odpovědi
1.	Jak značíme smíšený součin vektorů ?
2.	Co je výsledkem smíšeného součinu tří vektorů?	Číslo.
3.	Jaká je hodnota smíšeného součinu tří komplanárních vektorů?	Nula.
4.	Kdy je smíšený součin tří vektorů roven nule?	Jestliže vektory jsou komplanární.
5.	Jak se změní hodnota smíšeného součinu , jestliže zaměníme pořadí vektorů: ?	Znaménko bude opačné, došlo k záměně pořadí dvou řádků v determinantu.
6.	Jak se změní hodnota smíšeného součinu , jestliže zaměníme pořadí vektorů: ?	Hodnota se nezmění, došlo ke dvojnásobné záměně pořadí dvou řádků v determinantu
7.	Jak se změní hodnota smíšeného součinu , jestliže zaměníme pořadí vektorů: ?	Znaménko bude opačné, došlo k trojnásobné záměně pořadí dvou řádků v determinantu.
8.	Kdy je smíšený součin nezáporný?	Smíšený součin je nezáporný, následují-li vektory za sebou v kladné orientaci.
9.	Jak lze vypočítat velikost objemu rovnoběžnostěnu, který je sestrojen z nekomplanárních vektorů ?	Objem rovnoběžnostěnu je roven absolutní hodnotě smíšeného součinu vektorů .
10.	Jak lze vypočítat velikost objemu čtyřstěnu, který je sestrojen z nekomplanárních vektorů ?	Objem čtyřstěnu je roven jedné šestině absolutní hodnoty smíšeného součinu vektorů .

Č.	Úkoly	Řešení úkolů
1.	Předpokládejme vektory , , . Zapište vztah pro výpočet jejich smíšeného součinu .
2.	Vypočítejte smíšený součin vektorů , , .	, vektory jsou komplanární, 3. vektor je dán součtem 1. a 2. vektoru.
3.	Vypočítejte smíšený součin vektorů , , .	, při výpočtu determinantu v trojúhelníkovém tvaru pouze vynásobíme prvky na hlavní diagonále.