Přednášky        Zadání teoretických otázek a úkolů Řešení teoretických otázek a úkolů Vzorové řešené příklady Příklady na procvičení

1

1.1

1.2

1.3

1.4

1.5

1.6

1.6.1

1.6.2

1.6.3

1.6.4 Smíšený součin

Definice

Smíšeným součinem vektorů  nazýváme číslo (skalár) .

Věta

Pro smíšený součin vektorů , ,  platí:

1. ,

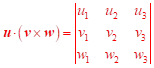2. ,

3. , ,

4. smíšený součin  je nezáporný právě tehdy, následují-li vektory  za sebou v kladné orientaci (proti směru chodu hodinových ručiček),

5. nejsou-li vektory komplanární, je absolutní hodnota jejich smíšeného součinu rovna objemu rovnoběžnostěnu sestrojeného z těchto vektorů,

Příklad

Vypočítejte smíšený součin vektorů ,  a .

6. objem příslušného čtyřstěnu je roven ,

7. jsou-li vektory komplanární, je smíšený součin roven nule.

Příklad

Vypočítejte objem čtyřstěnu s vrcholy , ,,.