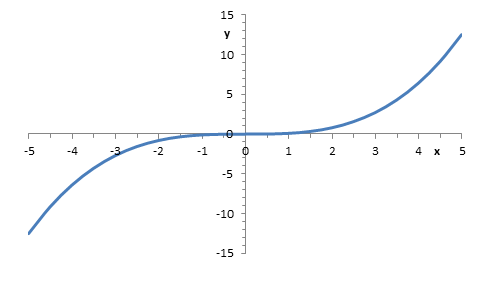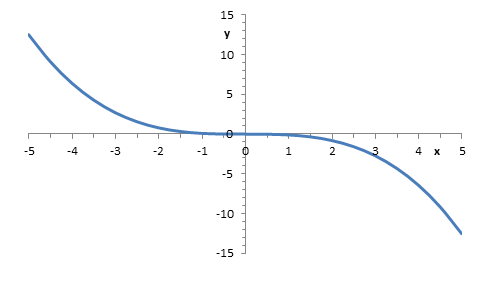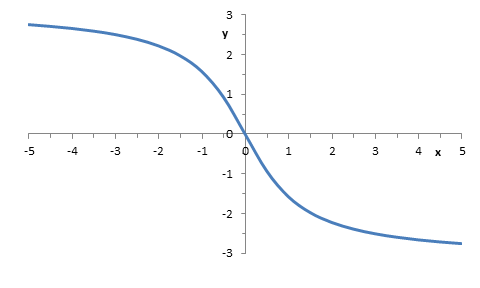Přednášky Zadání teoretických otázek a úkolů Řešení teoretických otázek a úkolů Vzorové řešené příklady Příklady na procvičení

4.6 Průběh funkce

Č.	Otázky	Odpovědi
1.	Jaké dva vztahy pro popis přímky používáme při sestavování rovnice tečny nebo normály ke grafu funkce?	nebo
2.	Co vyjadřuje koeficient v rovnici ?	Směrnici přímky.
3.	Co vyjadřuje koeficient v rovnici ?	Úsek na ose , který vytíná daná přímka.
4.	Co vyjadřuje koeficient v rovnici ?	Směrnici přímky.
5.	Co vyjadřují hodnoty v rovnici ?	Souřadnice bodu, kterým prochází daná přímka.
6.	Co mají společného dvě rovnoběžné přímky?	Směrnice rovnoběžných přímek jsou vzájemně totožné.
7.	Jaký je vztah mezi směrnicí tečny a směrnicí normály ke grafu zadané funkce ve zvoleném bodu.
8.	Co můžeme říci o funkci , pro kterou na intervalu platí: ?	Funkce je na intervalu rostoucí.
9.	Co můžeme říci o funkci , pro kterou na intervalu platí: ?	Funkce je na intervalu konstantní.
10.	Co můžeme říci o funkci , pro kterou na intervalu platí: ?	Funkce je na intervalu klesající.
11.	Co můžeme říci o funkci , jestliže existuje okolí bodu takové, že pro každý bod tohoto okolí platí: ?	Funkce je v bodu rostoucí.
12.	Co můžeme říci o funkci , jestliže existuje okolí bodu takové, že pro každý bod tohoto okolí platí: ?	Funkce je v bodu klesající.
13.	Co můžeme říci o funkci , jestliže existuje okolí bodu takové, že pro každý bod tohoto okolí platí: ?	Funkce má v bodu ostré lokální maximum.
14.	Co můžeme říci o funkci , jestliže existuje okolí bodu takové, že pro každý bod tohoto okolí platí: ?	Funkce má v bodu neostré lokální maximum.
15.	Co můžeme říci o funkci , jestliže existuje okolí bodu takové, že pro každý bod tohoto okolí platí: ?	Funkce má v bodu ostré lokální minimum.
16.	Co můžeme říci o funkci , jestliže existuje okolí bodu takové, že pro každý bod tohoto okolí platí: ?	Funkce má v bodu neostré lokální minimum.
17.	Co můžeme říci o funkci v bodu , jestliže má funkce v tomto bodu první derivaci kladnou?	Funkce je v bodu rostoucí.
18.	Co můžeme říci o funkci v bodu , jestliže má funkce v tomto bodu první derivaci rovnou nule?	Funkce je v bodu konstantní.
19.	Co můžeme říci o funkci v bodu , jestliže má funkce v tomto bodu zápornou první derivaci zápornou?	Funkce je v bodu klesající.
20.	Co to je stacionární bod?	Stacionární bod je bodem podezřelým z extrému.
21.	Jak nazýváme bod, který je podezřelý z extrému?	Bod, který je podezřelý z extrému, se nazývá stacionární bod.
22.	Jakou hodnotu nabývá první derivace funkce ve stacionárním bodu?	První derivace funkce ve stacionárním bodu je rovna nule.
23.	Jaká vlastnost funkce se mění v lokálním maximu?	V lokálním maximu se růst funkce mění v klesání.
24.	Jaká vlastnost funkce se mění v lokálním minimu?	V lokálním minimu se klesání funkce mění v růst.
25.	Jak určíme absolutní maximum funkce na uzavřeném intervalu?	Vybereme největší hodnotu ze všech lokálních maxim a funkčních hodnot v krajních bodech daného intervalu.
26.	Jak určíme absolutní minimum funkce na uzavřeném intervalu?	Vybereme nejmenší hodnotu ze všech lokálních minim a funkčních hodnot v krajních bodech daného intervalu.
27.	Co můžeme říci o funkci , o které víme, že na intervalu je její první derivace rostoucí?	Funkce je na intervalu konvexní.
28.	Co můžeme říci o funkci , o které víme, že na intervalu je její první derivace klesající?	Funkce je na intervalu konkávní.
29.	Co můžeme říci o funkci na intervalu , jestliže pro platí: ?	Funkce je na intervalu konvexní.
30.	Co můžeme říci o funkci na intervalu , jestliže pro platí: ?	Funkce je na intervalu konkávní.
31.	Co můžeme pro říci o funkci , o které víme, že všechny body jejího grafu leží nad tečnou sestrojenou v libovolném bodu ?	Funkce je na intervalu konvexní.
32.	Co můžeme pro říci o funkci , o které víme, že všechny body jejího grafu leží pod tečnou sestrojenou v libovolném bodu ?	Funkce je na intervalu konkávní.
33.	Co to je inflexní bod?	Inflexní bod je takový bod, ve kterém konvexní charakter funkce se mění na konkávní nebo naopak.
34.	Jak nazveme bod, ve kterém se konvexní charakter funkce mění na konkávní?	Inflexní bod.
35.	Jak nazveme bod, ve kterém se konkávní charakter funkce mění na konvexní?	Inflexní bod.
36.	Jak nazveme přímku , jestliže ?	Asymptota bez směrnice.
37.	Jak nazveme přímku , jestliže ?	Asymptota bez směrnice.
38.	Jak nazveme přímku , jestliže ?	Asymptota bez směrnice.
39.	Co z hlediska asymptot můžeme říci o funkci , o které víme, že ve vlastním bodu má nevlastní limitu?	Funkce má v daném vlastním bodu asymptotu bez směrnice.
40.	Co z hlediska asymptot můžeme říci o funkci , o které víme, že ve vlastním bodu má jednostrannou nevlastní limitu?	Funkce má v daném vlastním bodu asymptotu bez směrnice.
41.	Má funkce asymptotu? Pokud ano, napište její rovnici.
42.	Má funkce asymptotu? Pokud ano, napište její rovnici.
43.	Má funkce asymptotu? Pokud ano, napište její rovnici.
44.	Má funkce asymptotu? Pokud ano, napište její rovnici.
45.	Má funkce asymptoty? Pokud ano, napište jejich rovnice.	;
46.	Má funkce asymptoty? Pokud ano, napište jejich rovnice.	;
47.	Má funkce asymptoty? Pokud ano, napište jejich rovnice.	;

Č.	Úkoly	Řešení úkolů
1.	Z následujících výroků a vytvořte pravdivou ekvivalenci. Pokud by to nebylo možné, vytvořte pravdivou implikaci. : v každém bodu je , : funkce je na intervalu rostoucí.	Jestliže v každém bodu je , pak je funkce na intervalu rostoucí.
2.	Z následujících výroků a vytvořte pravdivou ekvivalenci. Pokud by to nebylo možné, vytvořte pravdivou implikaci. : v každém bodu je , : funkce je na intervalu klesající.	Jestliže v každém bodu je , pak je funkce na intervalu klesající.
3.	Z následujících výroků a vytvořte pravdivou ekvivalenci. Pokud by to nebylo možné, vytvořte pravdivou implikaci. : funkce je rostoucí v bodu , : existuje okolí bodu takové, že pro každý bod tohoto okolí platí: .	Funkce je rostoucí v bodu právě když existuje okolí bodu takové, že pro každý bod tohoto okolí platí: .
4.	Z následujících výroků a vytvořte pravdivou ekvivalenci. Pokud by to nebylo možné, vytvořte pravdivou implikaci. : funkce je klesající v bodu , : existuje okolí bodu takové, že pro každý bod tohoto okolí platí: .	Funkce je klesající v bodu právě když existuje okolí bodu takové, že pro každý bod tohoto okolí platí: .
5.	Z následujících výroků a vytvořte pravdivou ekvivalenci. Pokud by to nebylo možné, vytvořte pravdivou implikaci. : funkce má v bodu ostré lokální maximum, : existuje okolí bodu takové, že pro každý bod tohoto okolí platí: .	Funkce má v bodu ostré lokální maximum právě když existuje okolí bodu takové, že pro každý bod tohoto okolí platí: .
6.	Z následujících výroků a vytvořte pravdivou ekvivalenci. Pokud by to nebylo možné, vytvořte pravdivou implikaci. : funkce má v bodu neostré lokální maximum, : existuje okolí bodu takové, že pro každý bod tohoto okolí platí: .	Funkce má v bodu neostré lokální maximum právě když existuje okolí bodu takové, že pro každý bod tohoto okolí platí: .
7.	Z následujících výroků a vytvořte pravdivou ekvivalenci. Pokud by to nebylo možné, vytvořte pravdivou implikaci. : funkce má v bodu ostré lokální minimum, : existuje okolí bodu takové, že pro každý bod tohoto okolí platí: .	Funkce má v bodu ostré lokální minimum právě když existuje okolí bodu takové, že pro každý bod tohoto okolí platí: .
8.	Z následujících výroků a vytvořte pravdivou ekvivalenci. Pokud by to nebylo možné, vytvořte pravdivou implikaci. : funkce má v bodu neostré lokální minimum, : existuje okolí bodu takové, že pro každý bod tohoto okolí platí: .	Funkce má v bodu neostré lokální minimum právě když existuje okolí bodu takové, že pro každý bod tohoto okolí platí: .
9.	Z následujících výroků a vytvořte pravdivou ekvivalenci. Pokud by to nebylo možné, vytvořte pravdivou implikaci. : funkce je v bodu rostoucí, : funkce má v bodu kladnou první derivaci.	Jestliže funkce má v bodu kladnou první derivaci, pak funkce je v bodu rostoucí.
10.	Z následujících výroků a vytvořte pravdivou ekvivalenci. Pokud by to nebylo možné, vytvořte pravdivou implikaci. : funkce je v bodu klesající, : funkce má v bodu zápornou první derivaci.	Jestliže funkce má v bodu zápornou první derivaci, pak funkce je v bodu klesající.
11.	Z následujících výroků a vytvořte pravdivou ekvivalenci. Pokud by to nebylo možné, vytvořte pravdivou implikaci. : funkce je rostoucí na intervalu , : funkce je rostoucí ve všech bodech intervalu .	Funkce je rostoucí na intervalu právě když je rostoucí ve všech bodech intervalu .
12.	Z následujících výroků a vytvořte pravdivou ekvivalenci. Pokud by to nebylo možné, vytvořte pravdivou implikaci. : funkce je klesající na intervalu , : funkce je klesající ve všech bodech intervalu .	Funkce je klesající na intervalu právě když je klesající ve všech bodech intervalu .
13.	Za předpokladu, že funkce v bodu má ostrý lokální extrém, a že existuje , dopište vztah
14.	Za předpokladu, že funkce v bodu má neostrý lokální extrém, a že existuje , dopište vztah
15.	Za předpokladu, že pro funkci v bodu existuje , zapište nutnou podmínku existence lokálního maxima.
16.	Za předpokladu, že pro funkci v bodu existuje , zapište nutnou podmínku existence lokálního minima.
17.	Pomocí první derivace v okolí bodu zapište postačující podmínku existence lokálního maxima funkce ve stacionárním bodu .	Nalevo od stacionárního bodu je , napravo od stacionárního bodu je .
18.	Pomocí první derivace v okolí bodu zapište postačující podmínku existence lokálního minima funkce ve stacionárním bodu .	Nalevo od stacionárního bodu je , napravo od stacionárního bodu je .
19.	Z následujících výroků a vytvořte pravdivou ekvivalenci. Pokud by to nebylo možné, vytvořte pravdivou implikaci. : funkce je na intervalu konvexní, : první derivace funkce je na intervalu rostoucí.	Funkce je na intervalu konvexní právě když je první derivace funkce na intervalu rostoucí.
20.	Z následujících výroků a vytvořte pravdivou ekvivalenci. Pokud by to nebylo možné, vytvořte pravdivou implikaci. : funkce je na intervalu konkávní, : první derivace funkce je na intervalu klesající.	Funkce je na intervalu konkávní právě když je první derivace funkce na intervalu klesající.
21.	Pro funkci zapište postačující podmínku konvexnosti.	pro
22.	Pro funkci zapište postačující podmínku konkávnosti.	pro
23.	Za předpokladu, že existuje , zapište nutnou podmínku inflexe funkce v bodu .
24.	Pomocí druhé derivace (za předpokladu, že existuje) zapište postačující podmínku existence ostrého lokálního maxima funkce ve stacionárním bodu .
25.	Pomocí druhé derivace (za předpokladu, že existuje) zapište postačující podmínku existence ostrého lokálního minima funkce ve stacionárním bodu .
26.	Zapište vztah, pomocí kterého můžeme vypočítat hodnotu směrnice asymptoty se směrnicí ke grafu funkce .	resp. .
27.	Zapište vztah, pomocí kterého můžeme vypočítat hodnotu úseku , který na ose vytkne asymptota se s měrnicí ke grafu funkce .	resp.
28.	Zapište rovnici asymptoty funkce , o které víme, že ve vlastním bodu má nevlastní limitu.
29.	Zapište rovnici asymptoty funkce , o které víme, že ve vlastním bodu má jednostrannou nevlastní limitu.
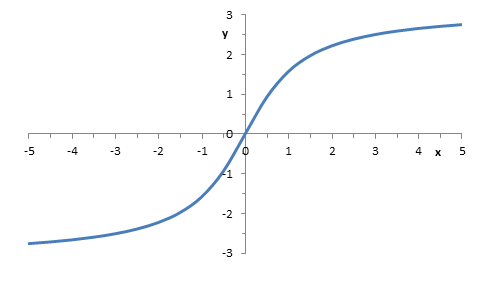
30.	Načrtněte možný průběh funkce v okolí bodu , jestliže v tomto okolí platí: a zároveň pro ; pro .	Funkce je rostoucí a přechází z konvexního do konkávního charakteru, takže bod je inflexním bodem.
31.	Načrtněte možný průběh funkce v okolí bodu , jestliže v tomto okolí platí: a zároveň pro ; pro .	Funkce je rostoucí a přechází z konkávního do konvexního charakteru, takže bod je inflexním bodem.
32.	Načrtněte možný průběh funkce v okolí bodu , jestliže v tomto okolí platí: a zároveň pro ; pro .	Funkce je klesající a přechází z konvexního do konkávního charakteru, takže bod je inflexním bodem.
33.	Načrtněte možný průběh funkce v okolí bodu , jestliže v tomto okolí platí: a zároveň pro ; pro .	Funkce je klesající a přechází z konkávního do konvexního charakteru, takže bod je inflexním bodem.
34.	Načrtněte možný průběh funkce v okolí bodu , jestliže v tomto okolí platí: a zároveň .	Bod je stacionárním bodem, funkce je konvexní, takže v bodu se nachází ostré lokální minimum.
35.	Načrtněte možný průběh funkce v okolí bodu , jestliže v tomto okolí platí: a zároveň .	Bod je stacionárním bodem, funkce je konkávní, takže v bodu se nachází ostré lokální maximum.