Přednášky Zadání teoretických otázek a úkolů Řešení teoretických otázek a úkolů Vzorové řešené příklady Příklady na procvičení
4.2 Věty o derivacích, diferencovatelnost
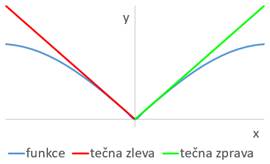
Existují-li jen navzájem různé jednostranné limity, pak mluvíme o jednostranných derivacích, tj.
derivace
zleva 
,
derivace zprava 
.
Věta
Funkce 
má
v bodu 
derivaci 
tehdy a jen tehdy, existují-li
jednostranné derivace zleva 
a zprava 
, pro které platí 
.
Věta: O vztahu derivace a spojitosti
Má-li funkce 
v bodu
derivaci, pak je funkce v bodu 
spojitá.
Na základě definice derivace funkce vypočtěte derivaci 
.
Přehled vzorců pro výpočet derivací základních funkcí
|
Konstanta |
|
|
Přirozená mocnina |
|
|
Obecná mocnina |
|
|
Exponenciální funkce |
|
|
|
|
|
Logaritmické funkce |
|
|
|
|
|
Goniometrické funkce |
|
|
|
|
|
|
|
|
|
|
|
Cyklometrické funkce |
|
|
|
|
|
|
|
|
|
|
Derivace funkce
, 
:
Jestliže 
na
intervalu 
, pak funkci 
, ,
nejprve přepíšeme do tvaru 
a potom funkci zderivujeme.
Vypočtěte derivace funkcí:
·
·
·
·
·
·
·
·
·
·
·
·
Věta: O výpočtu derivace konstantního násobku funkce, součtu, součinu a podílu funkcí
Jestliže mají funkce 
,
v bodu 
derivace 
,
, pak
je konstanta
pokud
Vypočtěte derivace funkcí:
·
·
·
Vypočtěte derivace funkcí:
·
·
·
·
·
·
Věta: O diferencovatelnosti
Má-li funkce v bodu
derivaci 
,
pak platí
,
kde 
.
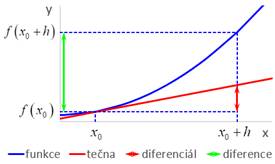
Diferenciál funkce
v bodu :
, kde
Diferenciál funkce 
v bodu
: 
Přírůstek funkce (diference)
,
kde
bývá nahrazován diferenciálem 
: 
Rozdíl mezi diferenciálem a diferencí
- diferenciál = přírůstek funkce do tečny ke grafu funkce
- diference = přírůstek funkce do funkční hodnoty
Tři různá tvrzení se stejným obsahem:
- funkce má
v bodu
derivaci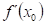 
, - funkce 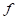má
v bodu 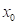diferenciál ,
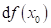- funkce 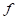je
v bodu 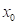diferencovatelná.
Pomocí diferenciálu odhadněte hodnotu funkce 
.
Věta: O derivaci složené funkce
Jestliže má vnitřní funkce 
derivaci
v bodu 
a vnější funkce má derivaci v bodu 
,
pak složená funkce 
má v bodu derivaci
Příklady
Vypočítejte derivace funkcí:
·
·
Vypočtěte derivace funkcí:
·
·
·
·
·
·
Věta: O derivaci inverzní funkce
Je-li funkce spojitá a
ryze monotónní na intervalu 
a má-li
funkce ve vnitřním bodu 
derivaci 
,
pak má inverzní funkce 
derivaci
v bodu 
a platí
,
kde
Příklad z praxe
Pohyb
kabiny výtahu je možno popsat jako rovnoměrně zrychlený pohyb rovnicí 
, kde 
je dráha, kterou
kabina výtahu vykonala v čase 
,
je zrychlení, 
je rychlost kabiny
výtahu na začátku sledovaného měření, tedy v čase 
, 
je výchozí dráha kabiny výtahu
v čase .
Předpokládejme, že na začátku pohybu se kabina výtahu
nachází v klidovém stavu v suterénu budovy, takže 
, 
. Na kabinu výtahu
působí zrychlení, které se v závislosti na čase 
mění: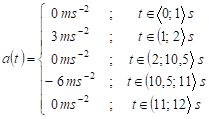 
.
Vytvořte vztahy popisující závislosti rychlosti 
na čase a dráhy kabiny výtahu na čase
. Načrtněte grafy
závislostí zrychlení 
,
rychlosti a dráhy kabiny výtahu na čase
. Předpokládejme, že
v kabině výtahu stojí osoba s hmotností 
. Vypočítejte, jak se mění relativní
tíha této osoby vzhledem ke kabině výtahu, kterou během pohybu kabiny výtahu
působí na její podlahu. Uvažujte tíhové zrychlení 
.
Příklad z praxe
Celkové
náklady 
výrobce jsou
závislé na produkci 
vyjádřené
počtem hotových výrobků podle vztahu 
.
Pomocí diferenciálu odhadněte změnu a hodnotu celkových
nákladů výrobce, jestliže počet výrobků klesne z 
na 
.