Přednášky Zadání teoretických otázek a úkolů Řešení teoretických otázek a úkolů Vzorové řešené příklady Příklady na procvičení

3.3 Limita a spojitost funkce

3.3.1 Limita funkce

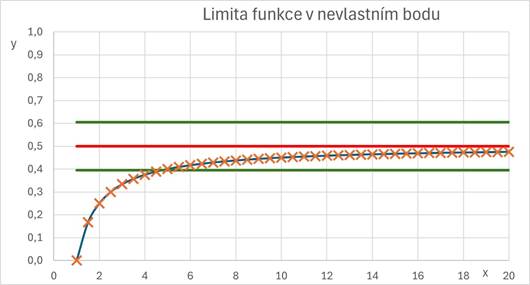
Limita funkce v nevlastním bodu .

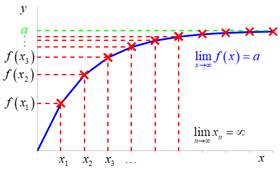
Definice

Říkáme, že limita funkce je pro rovna číslu a, píšeme , právě když pro každou posloupnost bodů s limitou platí, že posloupnost odpovídajících funkčních hodnot má limitu a, tedy .

Symbolicky:

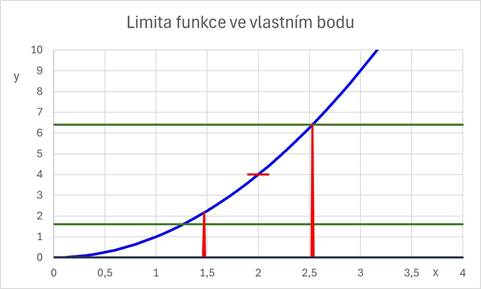
Limita funkce ve vlastním bodu .

Definice

Říkáme, že funkce má v bodu limitu rovnou číslu , píšeme , právě když pro každou posloupnost bodů s limitou platí, že posloupnost odpovídajících funkčních hodnot má limitu , tedy .

Symbolicky:

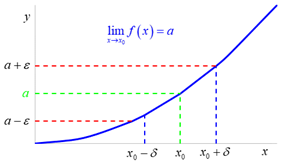
Cauchyova definice limity funkce ve vlastním bodu.

Říkáme, že funkce má v bodu limitu rovnou číslu , píšeme , právě když pro každé reálné kladné existuje reálné kladné takové, že platí: je-li z okolí bodu , pak absolutní hodnota rozdílu funkční hodnoty a čísla je menší než .

Symbolicky:

Jednostranné limity

limita zleva

limita zprava

Věta: Vztah mezi limitou v bodu a jednostrannými limitami

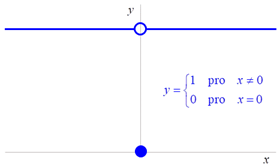
Věta: O počtu limit funkce v bodu

Funkce má v daném bodu nejvýše jednu limitu.

Věta: O limitě součtu, součinu a podílu funkcí

Jestliže , pak

limita součtu součet limit

limita součinu součin limit

limita podílu podíl limit

pokud , na určitém prstencovém okolí bodu .

Věta

Věta

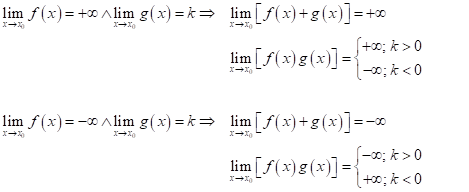
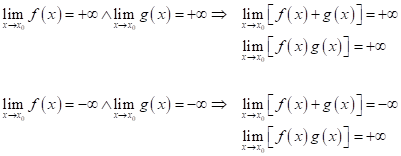
Věta: O limitě součinu ohraničené funkce a funkce s nulovou limitou

Jestliže a funkce je na určitém prstencovém okolí bodu ohraničená, pak

Věta: O limitě sevřené funkce

Jestliže na určitém prstencovém okolí bodu platí , přičemž , pak existuje limita sevřené funkce a je

Věta: O limitě složené funkce

Jestliže , přičemž na určitém prstencovém okolí bodu , , pak

Příklady

Vypočítejte: ; .

Věta: O vztahu nevlastní a nulové limity

Limitu kterékoliv elementární funkce v bodu jejího definičního oboru počítáme jako funkční hodnotu v tomto bodu.

Věta

Příklad

Vypočítejte .

Věta

;

Po dosazení za platí:

Příklad z praxe

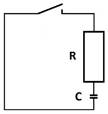Uvažujme rozpojený elektrický obvod, který obsahuje v sériovém zapojení nabitý kondenzátor, rezistor a spínač. Po uzavření obvodu se kondenzátor začne vybíjet přes rezistor. Časový průběh klesajícího napětí na kondenzátoru i rezistoru lze popsat rovnicí , kde je výchozí napětí nabitého kondenzátoru, je čas a je časová konstanta obvodu, jejíž hodnotu je možno vypočítat ze vztahu , kde je odpor rezistoru a je kapacita vybíjeného kondenzátoru.

Pro elektrický obvod s hodnotami: , a vypočítejte hodnotu ustáleného napětí na kondenzátoru pro čas blížící se k nekonečnu. Dále vypočítejte, za jak dlouho se napětí na kondenzátoru od dříve vypočtené ustálené hodnoty bude lišit o , resp. o . S využitím Ohmova zákona sestavte rovnici, která bude popisovat časový průběh vybíjecího proudu protékajícího rezistorem.