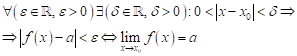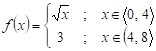Č.

Otázky

Odpovědi

1. 

Jak zapíšeme jednostrannou limitu zleva funkce  v bodu ?

2. 

Jak zapíšeme jednostrannou limitu zprava funkce  v bodu ?

3. 

Kolik limit v nevlastním bodu  může maximálně mít funkce jedné reálné proměnné?

Maximálně jednu.

4. 

Kolik limit v nevlastním bodu  může maximálně mít funkce jedné reálné proměnné?

Maximálně jednu.

5. 

Kolik limit ve vlastním bodu  může maximálně mít funkce jedné reálné proměnné?

Maximálně jednu.

6. 

Jak nazveme funkci jedné reálné proměnné, která má v nevlastním bodu  vlastní limitu?

Konvergentní funkce.

7. 

Jak nazveme funkci jedné reálné proměnné, která má v nevlastním bodu  vlastní limitu?

Konvergentní funkce.

8. 

Jak nazveme funkci jedné reálné proměnné, která má v nevlastním bodu  nevlastní limitu?

Divergentní funkce.

9. 

Jak nazveme funkci jedné reálné proměnné, která má v nevlastním bodu  nevlastní limitu?

Divergentní funkce.

10. 

Jak nazveme funkci jedné reálné proměnné, která nemá v nevlastním bodu  limitu?

Divergentní funkce.

11. 

Jak nazveme funkci jedné reálné proměnné, která nemá v nevlastním bodu  limitu?

Divergentní funkce.

12. 

Co můžeme říci o limitě v nevlastním bodu  konvergentní funkce jedné reálné proměnné?

Limita je vlastní.

13. 

Co můžeme říci o limitě v nevlastním bodu  konvergentní funkce jedné reálné proměnné?

Limita je vlastní.

14. 

Co můžeme říci o limitě v nevlastním bodu  divergentní funkce jedné reálné proměnné?

Limita je nevlastní nebo neexistuje.

15. 

Co můžeme říci o limitě v nevlastním bodu  divergentní funkce jedné reálné proměnné?

Limita je nevlastní nebo neexistuje.

16. 

Jak vypočteme limitu libovolné elementární funkce v bodu jejího definičního oboru?

Jako funkční hodnotu v daném bodu.

Č.

Úkoly

Řešení úkolů

1. 

Dopište následující definici

2. 

Dopište následující definici pro  

3. 

Dopište následující definici pro

4. 

Dopište následující definici pro

5. 

Za předpokladu, že , , dopište větu

6. 

Za předpokladu, že , , dopište větu

7. 

Za předpokladu, že , , ,  na určitém prstencovém okolí bodu , dopište větu

8. 

Za předpokladu, že , , dopište větu

9. 

Za předpokladu, že , , dopište větu

10. 

Za předpokladu, že , , dopište větu

11. 

Za předpokladu, že , , dopište větu

12. 

Za předpokladu, že , , dopište větu

13. 

Za předpokladu, že , , dopište větu

14. 

Za předpokladu, že , , dopište větu

15. 

Za předpokladu, že , , dopište větu

16. 

Za předpokladu, že , , dopište větu

17. 

Za předpokladu, že , , dopište větu

18. 

Za předpokladu, že , , dopište větu

19. 

Za předpokladu, že , , dopište větu

20. 

Vypočítejte .

21. 

Vypočítejte .

22. 

Vypočítejte .

23. 

Vypočítejte .

24. 

Vypočítejte .

25. 

Vypočítejte .

26. 

Vypočítejte .

27. 

Vypočítejte .

28. 

Vypočítejte .

29. 

Vypočítejte .

30. 

Vypočítejte .

 neexistuje

31. 

Vypočítejte .

32. 

Vypočítejte .

 neexistuje

33. 

Vypočítejte .

34. 

Vypočítejte .

 neexistuje

35. 

Vypočítejte .

36. 

Vypočítejte .

37. 

Vypočítejte .

 neexistuje

38. 

Vypočítejte .

39. 

Vypočítejte .

40. 

Vypočítejte .

41. 

Vypočítejte .

42. 

Vypočítejte .

43. 

Vypočítejte .

44. 

Vypočítejte .

45. 

Vypočítejte .

46. 

Vypočítejte .

47. 

Vypočítejte .

48. 

Vypočítejte .

49. 

Vypočítejte .

50. 

Vypočítejte .

51. 

Vypočítejte .

52. 

Vypočítejte .

53. 

Vypočítejte .

54. 

Vypočítejte .

55. 

Vypočítejte .

56. 

Vypočítejte .

57. 

Vypočítejte .

58. 

Vypočítejte .

59. 

Vypočítejte .

60. 

Vypočtěte  pro funkci .

61. 

Vypočtěte  pro funkci .

62. 

Vypočtěte  pro funkci .

63. 

Vypočtěte  pro funkci .

64. 

Vypočtěte  pro funkci .

 neexistuje, protože jednostranné limity nejsou stejné: , .

65. 

Vypočtěte  pro funkci .

66. 

Z následujících výroků  a  vytvořte pravdivou ekvivalenci. Pokud by to nebylo možné, vytvořte pravdivou implikaci.

,

.

67. 

Předpokládejme, že  a funkce  je na určitém prstencovém okolí bodu  ohraničená. Pak dopište vztah

68. 

Předpokládejme, že na určitém prstencovém okolí bodu  platí , přičemž . Pak dopište vztah

69. 

Předpokládejme, že  přičemž  na určitém prstencovém okolí bodu , a že . Pak dopište vztah

70. 

Předpokládejme, že . Vypočítejte hodnotu

71. 

Předpokládejme, že . Vypočítejte hodnotu

72. 

Dopište vztah

73. 

Dopište vztah

74. 

Dopište vztah

75. 

Dopište vztah