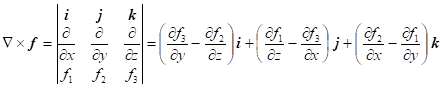Přednášky Zadání teoretických otázek a úkolů Řešení teoretických otázek a úkolů Vzorové řešené příklady Příklady na procvičení

1

2

2.1

2.2

2.3

2.4

2.5

2.6

2.7

2.8

2.9

2.10

2.11

2.12

2.13

2.14

2.15

2.16

2.17

2.18 Operátor nabla

Č.	Otázky	Odpovědi
1.	Uvažujme prostor , jehož každý bod je určen pomocí pravoúhlých souřadnic nebo pomocí polohového vektoru . Co to je vektorové pole a jak ho zapisujeme?	Vektorové pole je vektor (vektorová funkce) tří proměnných , který je definován na množině .
2.	Co to je Hamiltonův operátor nabla a jak ho značíme?	Je to symbolický vektor a značíme ho symbolem : .
3.	Jak nazýváme symbolický vektor ?	Hamiltonův operátor nabla.
4.	Jak nazýváme a jak znčíme skalární součin , kde je Hamiltonův operátor a je vektorové pole?	Divergence vektorového pole .
5.	Jak nazýváme a jak znčíme skalární součin , kde je Hamiltonův operátor a je vektorové pole?	Rotace vektorového pole .
6.	Co je to Laplaceův operátor delta a jak ho značíme?	Laplaceův operátor delta je symbolický skalární součin dvou Hamiltonových nabla operátorů
7.	Jak se nazývá symbolický skalární součin dvou Hamiltonových nabla operátorů ?	Laplaceův operátor delta.
8.	Jak jinak můžeme zapsat operaci , kde je Laplaceův operátor a je skalární pole?

Č.	Úkoly	Řešení úkolů
1.	Dopište vztah , kde je Hamiltonův operátor a je skalární pole třídy .
2.	Dopište vztah pro skalární součin , kde je Hamiltonův operátor a je vektorové pole třídy .
3.	Dopište vztah pro vektorový součin , kde je Hamiltonův operátor a je vektorové pole třídy .
4.	Předpokládejme Hamiltonův operátor , konstantu a skalární pole . Dopište vztah
5.	Předpokládejme Hamiltonův operátor , konstantu a vektorová pole . Dopište vztah
6.	Předpokládejme Hamiltonův operátor , konstantu a vektorová pole . Dopište vztah
7.	Předpokládejme Hamiltonův operátor a skalární pole . Dopište vztah
8.	Předpokládejme Hamiltonův operátor a vektorová pole . Dopište vztah
9.	Předpokládejme Hamiltonův operátor a vektorová pole . Dopište vztah
10.	Zapište definiční vztah pro Laplaceův operátor .
11.	Dopište vztah , kde je Laplaceův operátor a je skalární pole třídy .