Přednášky Zadání teoretických otázek a úkolů Řešení teoretických otázek a úkolů Vzorové řešené příklady Příklady na procvičení

1

2

2.1

2.2

2.3

2.4

2.5

2.6

2.7

2.8

2.9

2.10

2.11

2.12

2.13

2.14

2.15

2.16

2.17

2.18 Operátor nabla

Uvažujme prostor . Každému bodu z množiny přiřadíme jediný vektor

,

který nazýváme vektorové pole.

Definice

Operátor (nabla), nazývaný též Hamiltonovým operátorem, je „symbolickým vektorem“ o složkách .

Takže

.

Definice

Pro operátor definujeme následující operace:

1. ,

kde je skalární pole třídy ,

2. ,

kde je vektorové pole třídy ,

3. ,

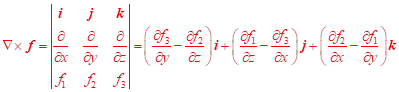kde je vektorové pole třídy .

Poznámka

Skalární součin nazýváme divergencí vektorového pole.

Vektorový součin nazýváme rotací vektorového pole.

Operátory mají následující vlastnosti:

,

,

,

,

,

,

kde je konstanta, a jsou skalární pole, a jsou vektorová pole.

Definice

Operátor

nazýváme Laplaceovým operátorem delta. Symbol , kde je skalární pole třídy , znamená .

Můžeme rovněž psát .