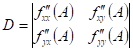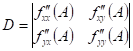|
Č.
|
Otázky
|
Odpovědi
|
|
1.
|
Co můžeme
říci o průběhu funkce  v bodu v bodu  , jestliže existuje takové okolí bodu , jestliže existuje takové okolí bodu  , že v něm platí , že v něm platí 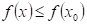 ? ?
|
Funkce  má v bodu má v bodu  neostré lokální
maximum. neostré lokální
maximum.
|
|
2.
|
Co můžeme
říci o průběhu funkce  v bodu v bodu  , jestliže existuje takové okolí bodu , jestliže existuje takové okolí bodu  , že v něm platí , že v něm platí 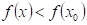 ? ?
|
Funkce  má v bodu má v bodu  ostré lokální
maximum. ostré lokální
maximum.
|
|
3.
|
Co můžeme
říci o průběhu funkce  v bodu v bodu  , jestliže existuje takové okolí bodu , jestliže existuje takové okolí bodu  , že v něm platí , že v něm platí 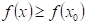 ? ?
|
Funkce  má v bodu má v bodu  neostré lokální
minimum. neostré lokální
minimum.
|
|
4.
|
Co můžeme
říci o průběhu funkce  v bodu v bodu  , jestliže existuje takové okolí bodu , jestliže existuje takové okolí bodu  , že v něm platí , že v něm platí 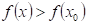 ? ?
|
Funkce  má v bodu má v bodu  ostré lokální
minimum. ostré lokální
minimum.
|
|
5.
|
Co můžeme
říci o průběhu funkce 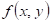 v bodu v bodu  , jestliže existuje takové okolí bodu , jestliže existuje takové okolí bodu  , že v něm platí , že v něm platí 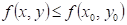 ? ?
|
Funkce 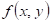 má v bodu má v bodu  neostré lokální
maximum. neostré lokální
maximum.
|
|
6.
|
Co můžeme
říci o průběhu funkce 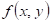 v bodu v bodu  , jestliže existuje takové okolí bodu , jestliže existuje takové okolí bodu 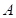 , že v něm platí , že v něm platí 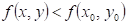 ? ?
|
Funkce 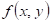 má v bodu má v bodu  ostré lokální
maximum. ostré lokální
maximum.
|
|
7.
|
Co můžeme
říci o průběhu funkce 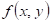 v bodu v bodu  , jestliže existuje takové okolí bodu , jestliže existuje takové okolí bodu  , že v něm platí , že v něm platí 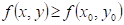 ? ?
|
Funkce 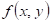 má v bodu má v bodu  neostré lokální
minimum. neostré lokální
minimum.
|
|
8.
|
Co můžeme
říci o průběhu funkce 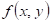 v bodu v bodu  , jestliže existuje takové okolí bodu , jestliže existuje takové okolí bodu  , že v něm platí , že v něm platí 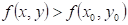 ? ?
|
Funkce 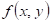 má v bodu má v bodu  ostré lokální
minimum. ostré lokální
minimum.
|
|
9.
|
Co můžeme
říci o průběhu funkce  v bodu v bodu 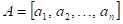 , jestliže existuje takové okolí bodu , jestliže existuje takové okolí bodu 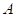 , že v něm platí , že v něm platí 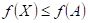 ? ?
|
Funkce  má v bodu má v bodu 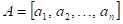 neostré lokální
maximum. neostré lokální
maximum.
|
|
10.
|
Co můžeme
říci o průběhu funkce  v bodu v bodu 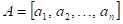 , jestliže existuje takové okolí bodu , jestliže existuje takové okolí bodu 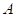 , že v něm platí , že v něm platí 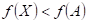 ? ?
|
Funkce  má v bodu má v bodu 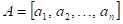 ostré lokální
maximum. ostré lokální
maximum.
|
|
11.
|
Co můžeme
říci o průběhu funkce  v bodu v bodu 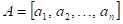 , jestliže existuje takové okolí bodu , jestliže existuje takové okolí bodu 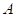 , že v něm platí , že v něm platí 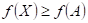 ? ?
|
Funkce  má v bodu má v bodu 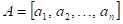 neostré lokální
minimum. neostré lokální
minimum.
|
|
12.
|
Co můžeme
říci o průběhu funkce  v bodu v bodu 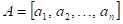 , jestliže existuje takové okolí bodu , jestliže existuje takové okolí bodu 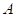 , že v něm platí , že v něm platí 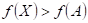 ? ?
|
Funkce  má v bodu má v bodu 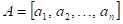 ostré lokální
minimum. ostré lokální
minimum.
|
|
13.
|
Co můžeme
říci o průběhu funkce  v bodu v bodu  , jestliže platí následující vztah: , jestliže platí následující vztah: 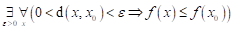 ? ?
|
Funkce  má v bodu má v bodu  neostré lokální
maximum. neostré lokální
maximum.
|
|
14.
|
Co můžeme
říci o průběhu funkce  v bodu v bodu  , jestliže platí následující vztah: , jestliže platí následující vztah: 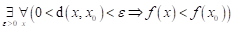 ? ?
|
Funkce  má v bodu má v bodu  ostré lokální
maximum. ostré lokální
maximum.
|
|
15.
|
Co můžeme
říci o průběhu funkce  v bodu v bodu  , jestliže platí následující vztah: , jestliže platí následující vztah: 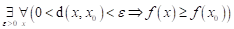 ? ?
|
Funkce  má v bodu má v bodu  neostré lokální
minimum. neostré lokální
minimum.
|
|
16.
|
Co můžeme
říci o průběhu funkce  v bodu v bodu  , jestliže platí následující vztah: , jestliže platí následující vztah: 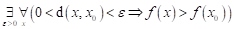 ? ?
|
Funkce  má v bodu má v bodu  ostré lokální
minimum. ostré lokální
minimum.
|
|
17.
|
Co můžeme
říci o průběhu funkce 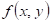 v bodu v bodu  , jestliže platí následující vztah: , jestliže platí následující vztah: 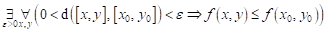 ? ?
|
Funkce 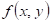 má v bodu má v bodu  neostré lokální
maximum. neostré lokální
maximum.
|
|
18.
|
Co můžeme
říci o průběhu funkce 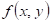 v bodu v bodu  , jestliže platí následující vztah: , jestliže platí následující vztah: 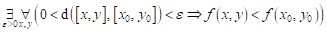 ? ?
|
Funkce 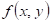 má v bodu má v bodu  ostré lokální
maximum. ostré lokální
maximum.
|
|
19.
|
Co můžeme
říci o průběhu funkce 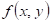 v bodu v bodu  , jestliže platí následující vztah: , jestliže platí následující vztah: 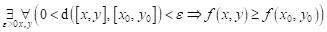 ? ?
|
Funkce 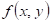 má v bodu má v bodu  neostré lokální
minimum. neostré lokální
minimum.
|
|
20.
|
Co můžeme
říci o průběhu funkce 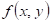 v bodu v bodu  , jestliže platí následující vztah: , jestliže platí následující vztah: 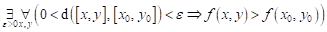 ? ?
|
Funkce 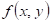 má v bodu má v bodu  ostré lokální
minimum. ostré lokální
minimum.
|
|
21.
|
Co můžeme
říci o průběhu funkce  v bodu v bodu 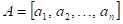 , jestliže platí následující vztah: , jestliže platí následující vztah: 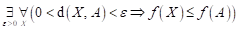 ? ?
|
Funkce  má v bodu má v bodu 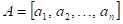 neostré lokální
maximum. neostré lokální
maximum.
|
|
22.
|
Co můžeme
říci o průběhu funkce  v bodu v bodu 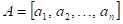 , jestliže platí následující vztah: , jestliže platí následující vztah: 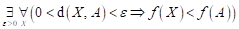 ? ?
|
Funkce  má v bodu má v bodu 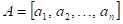 ostré lokální
maximum. ostré lokální
maximum.
|
|
23.
|
Co můžeme
říci o průběhu funkce  v bodu v bodu 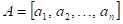 , jestliže platí následující vztah: , jestliže platí následující vztah: 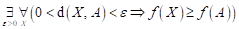 ? ?
|
Funkce  má v bodu má v bodu 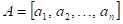 neostré lokální
minimum. neostré lokální
minimum.
|
|
24.
|
Co můžeme
říci o průběhu funkce  v bodu v bodu 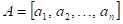 , jestliže platí následující vztah: , jestliže platí následující vztah: 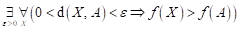 ? ?
|
Funkce  má v bodu má v bodu 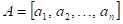 ostré lokální
minimum. ostré lokální
minimum.
|
|
25.
|
Co můžeme
říci o hodnotě derivace 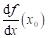 , funkce , funkce  v bodu v bodu  , ve kterém má daná funkce lokální extrém? , ve kterém má daná funkce lokální extrém?
|
Pokud tato
derivace v bodu 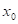 s lokálním
extrémem existuje, pak je rovna nule: s lokálním
extrémem existuje, pak je rovna nule: 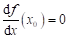 . .
|
|
26.
|
Co můžeme
říci o hodnotách parciálních derivací 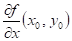 , , 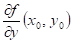 funkce funkce 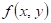 v bodu v bodu  , ve kterém má daná funkce lokální extrém? , ve kterém má daná funkce lokální extrém?
|
Pokud tyto
derivace v bodu  s lokálním
extrémem existují, pak jsou obě rovny nule: s lokálním
extrémem existují, pak jsou obě rovny nule: 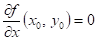 , , 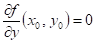 . .
|
|
27.
|
Co můžeme
říci o hodnotách parciálních derivací 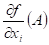 , , 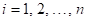 funkce funkce  v bodu v bodu 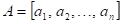 , ve kterém má daná funkce lokální extrém? , ve kterém má daná funkce lokální extrém?
|
Pokud tyto
derivace v bodu s lokálním extrémem existují, pak jsou všechny
rovny nule: 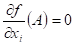 , , 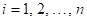 . .
|
|
28.
|
Jak se nazývá
bod  , ve kterém pro funkci , ve kterém pro funkci  platí: platí: 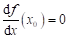 ? ?
|
Bod 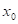 se nazývá
stacionární bod funkce se nazývá
stacionární bod funkce  . .
|
|
29.
|
Jak se nazývá
bod  , ve kterém pro funkci , ve kterém pro funkci 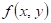 platí: platí: 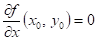 , , 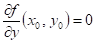 ? ?
|
Bod  se nazývá
stacionární bod funkce se nazývá
stacionární bod funkce 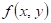 . .
|
|
30.
|
Jak se nazývá
bod 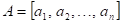 , ve kterém pro funkci , ve kterém pro funkci 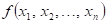 platí: platí: 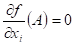 pro všechna pro všechna 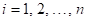 ? ?
|
Bod 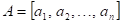 se nazývá
stacionární bod funkce se nazývá
stacionární bod funkce  . .
|
|
31.
|
Co to je stacionární
bod funkce  ? ?
|
Stacionární
bod funkce  je bod podezřelý
z extrému. je bod podezřelý
z extrému.
|
|
32.
|
Co to je stacionární
bod funkce 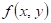 ? ?
|
Stacionární
bod funkce 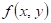 je bod podezřelý
z extrému. je bod podezřelý
z extrému.
|
|
33.
|
Co to je stacionární
bod funkce  ? ?
|
Stacionární
bod funkce  je bod podezřelý
z extrému. je bod podezřelý
z extrému.
|
|
34.
|
Co můžeme
říci o hodnotě derivace 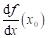 funkce funkce  ve stacionárním bodu ve stacionárním bodu
 ? ?
|
Derivace ve
stacionárním bodu 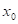 je rovna nule: je rovna nule: 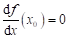 . .
|
|
35.
|
Co můžeme
říci o hodnotách parciálních derivací funkce 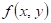 ve stacionárním bodu ve stacionárním bodu
 ? ?
|
Derivace ve
stacionárním bodu  jsou obě rovny nule: jsou obě rovny nule:
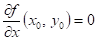 , , 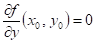 . .
|
|
36.
|
Co můžeme
říci o hodnotách parciálních derivací 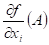 , , 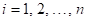 funkce funkce  ve stacionárním bodu ve stacionárním bodu
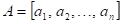 ? ?
|
Derivace ve
stacionárním bodu 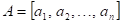 jsou všechny rovny
nule: jsou všechny rovny
nule: 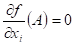 , , 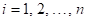 . .
|
|
37.
|
Předpokládejme,
že v daném bodu 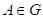 , kde , kde 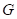 je libovolné okolí
bodu je libovolné okolí
bodu 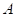 , je , je 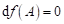 , , 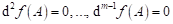 pro pro 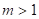 , ale že , ale že 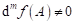 , přičemž , přičemž 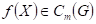 . Co z hlediska existence extrému funkce . Co z hlediska existence extrému funkce 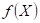 v bodu v bodu 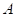 můžeme říci,
jestliže můžeme říci,
jestliže 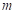 je liché číslo? je liché číslo?
|
Funkce 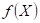 nemá v bodu nemá v bodu 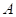 extrém. extrém.
|
|
38.
|
Předpokládejme,
že v daném bodu 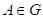 , kde , kde 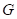 je libovolné okolí
bodu je libovolné okolí
bodu 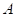 , je , je 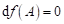 , , 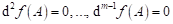 pro pro 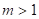 , ale že , ale že 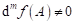 , přičemž , přičemž 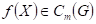 . Co z hlediska existence extrému funkce . Co z hlediska existence extrému funkce 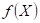 v bodu v bodu 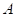 můžeme říci,
jestliže můžeme říci,
jestliže 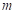 je sudé číslo a jestliže
pro každý bod je sudé číslo a jestliže
pro každý bod 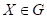 , , 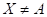 je je 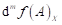 kladný? kladný?
|
Funkce 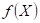 má v bodu má v bodu 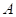 lokální minimum. lokální minimum.
|
|
39.
|
Předpokládejme,
že v daném bodu 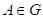 , kde , kde 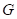 je libovolné okolí
bodu je libovolné okolí
bodu 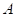 , je , je 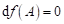 , , 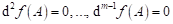 pro pro 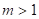 , ale že , ale že 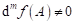 , přičemž , přičemž 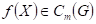 . Co z hlediska existence extrému funkce . Co z hlediska existence extrému funkce 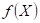 v bodu v bodu 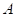 můžeme říci,
jestliže můžeme říci,
jestliže 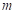 je sudé číslo a jestliže
pro každý bod je sudé číslo a jestliže
pro každý bod 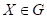 , , 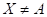 je je 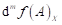 záporný? záporný?
|
Funkce 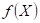 má v bodu má v bodu 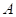 lokální maximum. lokální maximum.
|
|
40.
|
Předpokládejme,
že v daném bodu 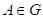 , kde , kde 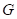 je libovolné okolí
bodu je libovolné okolí
bodu 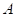 , je , je 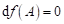 , , 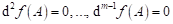 pro pro 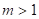 , ale že , ale že 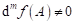 , přičemž , přičemž 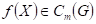 . Co z hlediska existence extrému funkce . Co z hlediska existence extrému funkce 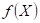 v bodu v bodu 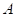 můžeme říci,
jestliže můžeme říci,
jestliže 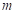 je sudé číslo a jestliže
existují body je sudé číslo a jestliže
existují body 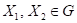 tak, že tak, že 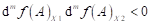 ? ?
|
Funkce 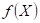 nemá v bodu nemá v bodu 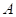 extrém. extrém.
|
|
41.
|
Předpokládejme funkci 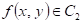 , bod , bod 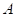 , který je jejím stacionárním bodem a determinant , který je jejím stacionárním bodem a determinant 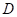 , který obsahuje příslušné derivace druhého řádu: , který obsahuje příslušné derivace druhého řádu: 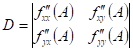 . .
Co z hlediska extrémů můžeme říci, jestliže 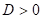 a a 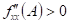 ? ?
|
Funkce 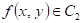 má v bodu má v bodu 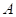 ostré lokální
minimum. ostré lokální
minimum.
|
|
42.
|
Předpokládejme funkci 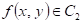 , bod , bod 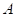 , který je jejím stacionárním bodem a determinant , který je jejím stacionárním bodem a determinant 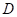 , který obsahuje příslušné derivace druhého řádu: , který obsahuje příslušné derivace druhého řádu: 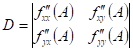 . .
Co z hlediska extrémů můžeme říci, jestliže 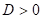 a a 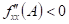 ? ?
|
Funkce 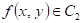 má v bodu má v bodu 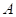 ostré lokální
maximum. ostré lokální
maximum.
|
|
43.
|
Předpokládejme funkci 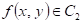 , bod , bod 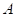 , který je jejím stacionárním bodem a determinant , který je jejím stacionárním bodem a determinant 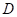 , který obsahuje příslušné derivace druhého řádu: , který obsahuje příslušné derivace druhého řádu: 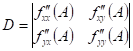 . .
Co z hlediska extrémů můžeme říci, jestliže 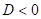 ? ?
|
Funkce 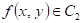 nemá v bodu nemá v bodu 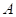 lokální extrém. lokální extrém.
|
|
44.
|
Předpokládejme funkci 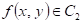 , bod , bod 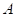 , který je jejím stacionárním bodem a determinant , který je jejím stacionárním bodem a determinant 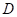 , který obsahuje příslušné derivace druhého řádu: , který obsahuje příslušné derivace druhého řádu: 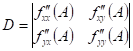 . .
Co z hlediska extrémů můžeme říci, jestliže 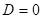 ? ?
|
Na základě
znalostí prvních a druhých derivací funkce 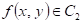 v bodu v bodu 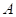 v tomto případě
nelze rozhodnout o existenci lokálního extrému. v tomto případě
nelze rozhodnout o existenci lokálního extrému.
|
|
Č.
|
Úkoly
|
Řešení úkolů
|
|
1.
|
Z
následujících výroků 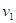 a a 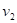 vytvořte pravdivou
ekvivalenci. Pokud by to nebylo možné, vytvořte pravdivou implikaci. vytvořte pravdivou
ekvivalenci. Pokud by to nebylo možné, vytvořte pravdivou implikaci.
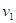 : funkce : funkce 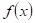 má v bodu má v bodu 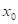 neostré lokální
maximum, neostré lokální
maximum,
 : existuje takové okolí bodu : existuje takové okolí bodu 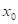 , že v něm platí , že v něm platí 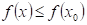 . .
|
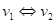
Funkce 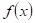 má v bodu má v bodu 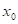 neostré lokální
maximum, právě když existuje takové okolí bodu neostré lokální
maximum, právě když existuje takové okolí bodu 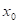 , že v něm platí , že v něm platí 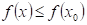 . .
|
|
2.
|
Z
následujících výroků 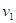 a a  vytvořte pravdivou
ekvivalenci. Pokud by to nebylo možné, vytvořte pravdivou implikaci. vytvořte pravdivou
ekvivalenci. Pokud by to nebylo možné, vytvořte pravdivou implikaci.
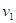 : funkce : funkce 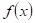 má v bodu má v bodu 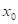 ostré lokální
maximum, ostré lokální
maximum,
 : existuje takové okolí bodu : existuje takové okolí bodu 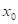 , že v něm platí , že v něm platí 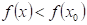 . .
|
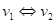
Funkce 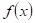 má v bodu má v bodu 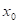 ostré lokální
maximum, právě když existuje takové okolí bodu ostré lokální
maximum, právě když existuje takové okolí bodu 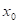 , že v něm platí , že v něm platí 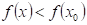 . .
|
|
3.
|
Z
následujících výroků 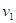 a a  vytvořte pravdivou
ekvivalenci. Pokud by to nebylo možné, vytvořte pravdivou implikaci. vytvořte pravdivou
ekvivalenci. Pokud by to nebylo možné, vytvořte pravdivou implikaci.
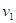 : funkce : funkce 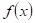 má v bodu má v bodu 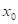 neostré lokální minimum, neostré lokální minimum,
 : existuje takové okolí bodu : existuje takové okolí bodu 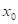 , že v něm platí , že v něm platí 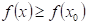 . .
|
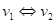
Funkce 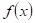 má v bodu má v bodu 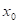 neostré lokální minimum,
právě když existuje takové okolí bodu neostré lokální minimum,
právě když existuje takové okolí bodu 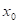 , že v něm platí , že v něm platí 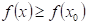 . .
|
|
4.
|
Z
následujících výroků 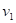 a a  vytvořte pravdivou
ekvivalenci. Pokud by to nebylo možné, vytvořte pravdivou implikaci. vytvořte pravdivou
ekvivalenci. Pokud by to nebylo možné, vytvořte pravdivou implikaci.
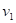 : funkce : funkce 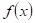 má v bodu má v bodu 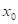 ostré lokální minimum, ostré lokální minimum,
 : existuje takové okolí bodu : existuje takové okolí bodu 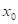 , že v něm platí , že v něm platí 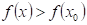 . .
|
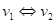
Funkce 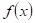 má v bodu má v bodu 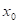 ostré lokální minimum,
právě když existuje takové okolí bodu ostré lokální minimum,
právě když existuje takové okolí bodu 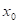 , že v něm platí , že v něm platí 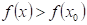 . .
|
|
5.
|
Z
následujících výroků 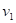 a a  vytvořte pravdivou
ekvivalenci. Pokud by to nebylo možné, vytvořte pravdivou implikaci. vytvořte pravdivou
ekvivalenci. Pokud by to nebylo možné, vytvořte pravdivou implikaci.
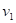 : funkce : funkce 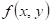 má v bodu má v bodu 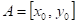 neostré lokální
maximum, neostré lokální
maximum,
 : existuje takové okolí bodu : existuje takové okolí bodu 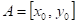 , že v něm platí , že v něm platí 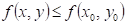 . .
|
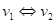
Funkce 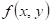 má v bodu má v bodu 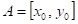 neostré lokální
maximum, právě když existuje takové okolí bodu neostré lokální
maximum, právě když existuje takové okolí bodu 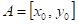 , že v něm platí , že v něm platí 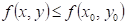 . .
|
|
6.
|
Z
následujících výroků 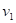 a a  vytvořte pravdivou
ekvivalenci. Pokud by to nebylo možné, vytvořte pravdivou implikaci. vytvořte pravdivou
ekvivalenci. Pokud by to nebylo možné, vytvořte pravdivou implikaci.
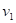 : funkce : funkce 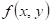 má v bodu má v bodu 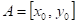 ostré lokální
maximum, ostré lokální
maximum,
 : existuje takové okolí bodu : existuje takové okolí bodu 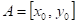 , že v něm platí , že v něm platí 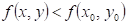 . .
|
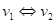
Funkce 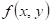 má v bodu má v bodu 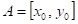 ostré lokální
maximum, právě když existuje takové okolí bodu ostré lokální
maximum, právě když existuje takové okolí bodu 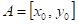 , že v něm platí , že v něm platí 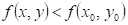 . .
|
|
7.
|
Z
následujících výroků 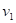 a a  vytvořte pravdivou
ekvivalenci. Pokud by to nebylo možné, vytvořte pravdivou implikaci. vytvořte pravdivou
ekvivalenci. Pokud by to nebylo možné, vytvořte pravdivou implikaci.
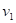 : funkce : funkce 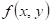 má v bodu má v bodu 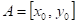 neostré lokální minimum, neostré lokální minimum,
 : existuje takové okolí bodu : existuje takové okolí bodu 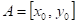 , že v něm platí , že v něm platí 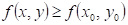 . .
|
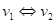
Funkce 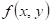 má v bodu má v bodu 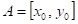 neostré lokální minimum,
právě když existuje takové okolí bodu neostré lokální minimum,
právě když existuje takové okolí bodu 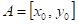 , že v něm platí , že v něm platí 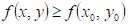 . .
|
|
8.
|
Z
následujících výroků 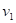 a a  vytvořte pravdivou
ekvivalenci. Pokud by to nebylo možné, vytvořte pravdivou implikaci. vytvořte pravdivou
ekvivalenci. Pokud by to nebylo možné, vytvořte pravdivou implikaci.
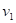 : funkce : funkce 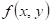 má v bodu má v bodu 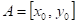 ostré lokální minimum, ostré lokální minimum,
 : existuje takové okolí bodu : existuje takové okolí bodu 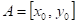 , že v něm platí , že v něm platí 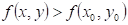 . .
|
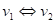
Funkce 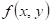 má v bodu má v bodu 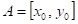 ostré lokální minimum,
právě když existuje takové okolí bodu ostré lokální minimum,
právě když existuje takové okolí bodu 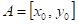 , že v něm platí , že v něm platí 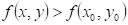 . .
|
|
9.
|
Z
následujících výroků 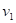 a a  vytvořte pravdivou
ekvivalenci. Pokud by to nebylo možné, vytvořte pravdivou implikaci. vytvořte pravdivou
ekvivalenci. Pokud by to nebylo možné, vytvořte pravdivou implikaci.
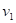 : funkce : funkce 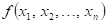 má v bodu má v bodu 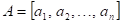 neostré lokální
maximum, neostré lokální
maximum,
 : existuje takové okolí bodu : existuje takové okolí bodu 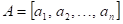 , že v něm platí , že v něm platí 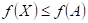 . .
|
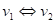
Funkce 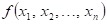 má v bodu má v bodu 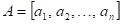 neostré lokální
maximum, právě když existuje takové okolí bodu neostré lokální
maximum, právě když existuje takové okolí bodu 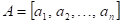 , že v něm platí , že v něm platí 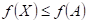 . .
|
|
10.
|
Z
následujících výroků 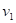 a a  vytvořte pravdivou
ekvivalenci. Pokud by to nebylo možné, vytvořte pravdivou implikaci. vytvořte pravdivou
ekvivalenci. Pokud by to nebylo možné, vytvořte pravdivou implikaci.
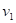 : funkce : funkce 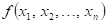 má v bodu má v bodu 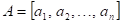 ostré lokální
maximum, ostré lokální
maximum,
 : existuje takové okolí bodu : existuje takové okolí bodu 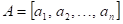 , že v něm platí , že v něm platí 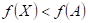 . .
|
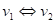
Funkce 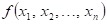 má v bodu má v bodu 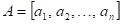 ostré lokální
maximum, právě když existuje takové okolí bodu ostré lokální
maximum, právě když existuje takové okolí bodu 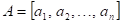 , že v něm platí , že v něm platí 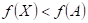 . .
|
|
11.
|
Z
následujících výroků 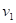 a a  vytvořte pravdivou
ekvivalenci. Pokud by to nebylo možné, vytvořte pravdivou implikaci. vytvořte pravdivou
ekvivalenci. Pokud by to nebylo možné, vytvořte pravdivou implikaci.
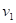 : funkce : funkce 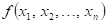 má v bodu má v bodu 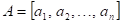 neostré lokální minimum, neostré lokální minimum,
 : existuje takové okolí bodu : existuje takové okolí bodu 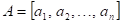 , že v něm platí , že v něm platí 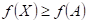 . .
|
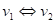
Funkce 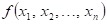 má v bodu má v bodu 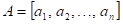 neostré lokální minimum,
právě když existuje takové okolí bodu neostré lokální minimum,
právě když existuje takové okolí bodu 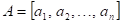 , že v něm platí , že v něm platí 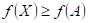 . .
|
|
12.
|
Z
následujících výroků 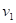 a a  vytvořte pravdivou
ekvivalenci. Pokud by to nebylo možné, vytvořte pravdivou implikaci. vytvořte pravdivou
ekvivalenci. Pokud by to nebylo možné, vytvořte pravdivou implikaci.
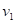 : funkce : funkce 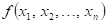 má v bodu má v bodu 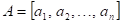 ostré lokální minimum, ostré lokální minimum,
 : existuje takové okolí bodu : existuje takové okolí bodu 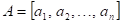 , že v něm platí , že v něm platí 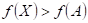 . .
|
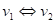
Funkce 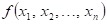 má v bodu má v bodu 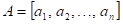 ostré lokální minimum,
právě když existuje takové okolí bodu ostré lokální minimum,
právě když existuje takové okolí bodu 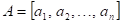 , že v něm platí , že v něm platí  . .
|
|
13.
|
Dopište
následující tvrzení: 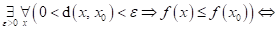
|
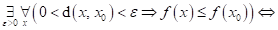 funkce funkce 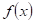
má v bodu
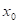 neostré lokální
maximum. neostré lokální
maximum.
|
|
14.
|
Dopište
následující tvrzení: 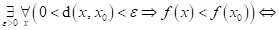
|
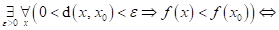 funkce funkce 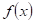
má v bodu
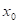 ostré lokální
maximum. ostré lokální
maximum.
|
|
15.
|
Dopište
následující tvrzení: 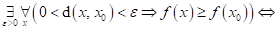
|
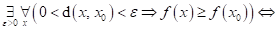 funkce funkce 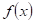
má v bodu
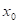 neostré lokální
minimum. neostré lokální
minimum.
|
|
16.
|
Dopište
následující tvrzení: 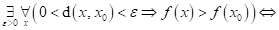
|
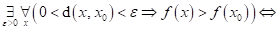 funkce funkce 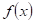
má v bodu
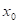 ostré lokální
minimum. ostré lokální
minimum.
|
|
17.
|
Dopište
následující tvrzení: 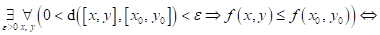
|
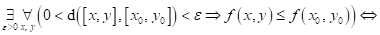 funkce funkce 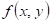
má v bodu
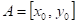 neostré lokální
maximum. neostré lokální
maximum.
|
|
18.
|
Dopište
následující tvrzení: 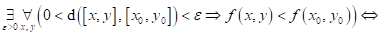
|
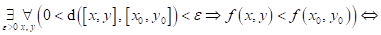 funkce funkce 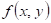
má v bodu
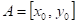 ostré lokální
maximum. ostré lokální
maximum.
|
|
19.
|
Dopište
následující tvrzení: 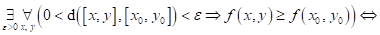
|
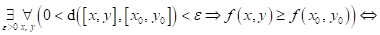 funkce funkce 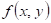
má v bodu
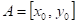 neostré lokální
minimum. neostré lokální
minimum.
|
|
20.
|
Dopište
následující tvrzení: 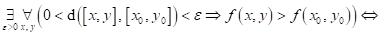
|
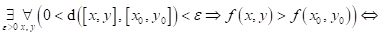 funkce funkce 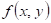
má v bodu
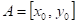 ostré lokální
minimum. ostré lokální
minimum.
|
|
21.
|
Dopište
následující tvrzení: 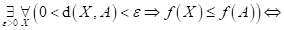
|
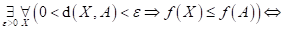 funkce funkce 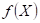
má v bodu
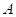 neostré lokální
maximum. neostré lokální
maximum.
|
|
22.
|
Dopište
následující tvrzení: 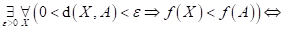
|
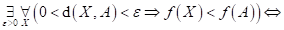 funkce funkce 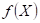
má v bodu
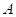 ostré lokální
maximum. ostré lokální
maximum.
|
|
23.
|
Dopište
následující tvrzení: 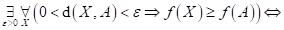
|
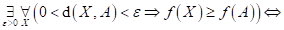 funkce funkce 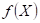
má v bodu
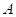 neostré lokální
minimum. neostré lokální
minimum.
|
|
24.
|
Dopište
následující tvrzení: 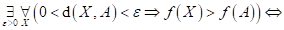
|
 funkce funkce 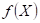
má v bodu
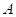 ostré lokální
minimum. ostré lokální
minimum.
|
|
25.
|
Doplňte
vhodné relační znaménko: funkce 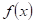 má v bodu má v bodu 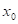 ostré lokální
maximum, právě když existuje takové okolí bodu ostré lokální
maximum, právě když existuje takové okolí bodu 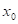 , že v něm platí , že v něm platí 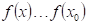 . .
|
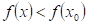
|
|
26.
|
Doplňte
vhodné relační znaménko: funkce 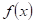 má v bodu má v bodu 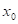 neostré lokální
maximum, právě když existuje takové okolí bodu neostré lokální
maximum, právě když existuje takové okolí bodu 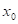 , že v něm platí , že v něm platí 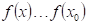 . .
|
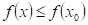
|
|
27.
|
Doplňte
vhodné relační znaménko: funkce 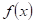 má v bodu má v bodu 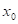 ostré lokální minimum,
právě když existuje takové okolí bodu ostré lokální minimum,
právě když existuje takové okolí bodu 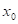 , že v něm platí , že v něm platí 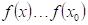 . .
|

|
|
28.
|
Doplňte
vhodné relační znaménko: funkce 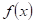 má v bodu má v bodu 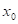 neostré lokální minimum,
právě když existuje takové okolí bodu neostré lokální minimum,
právě když existuje takové okolí bodu 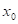 , že v něm platí , že v něm platí 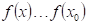 . .
|
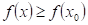
|
|
29.
|
Doplňte
vhodné relační znaménko: funkce 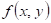 má v bodu má v bodu 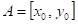 ostré lokální
maximum, právě když existuje takové okolí bodu ostré lokální
maximum, právě když existuje takové okolí bodu 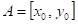 , že v něm platí , že v něm platí 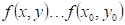 . .
|

|
|
30.
|
Doplňte
vhodné relační znaménko: funkce 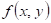 má v bodu má v bodu 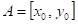 neostré lokální
maximum, právě když existuje takové okolí bodu neostré lokální
maximum, právě když existuje takové okolí bodu 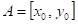 , že v něm platí , že v něm platí 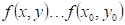 . .
|
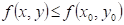
|
|
31.
|
Doplňte
vhodné relační znaménko: funkce 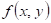 má v bodu má v bodu 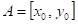 ostré lokální minimum,
právě když existuje takové okolí bodu ostré lokální minimum,
právě když existuje takové okolí bodu 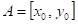 , že v něm platí , že v něm platí  . .
|
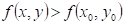
|
|
32.
|
Doplňte
vhodné relační znaménko: funkce 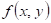 má v bodu má v bodu 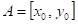 neostré lokální minimum,
právě když existuje takové okolí bodu neostré lokální minimum,
právě když existuje takové okolí bodu 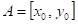 , že v něm platí , že v něm platí 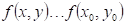 . .
|
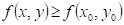
|
|
33.
|
Doplňte
vhodné relační znaménko: funkce 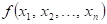 má v bodu má v bodu 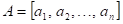 ostré lokální
maximum, právě když existuje takové okolí bodu ostré lokální
maximum, právě když existuje takové okolí bodu 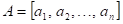 , že v něm platí , že v něm platí 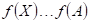 . .
|
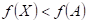
|
|
34.
|
Doplňte
vhodné relační znaménko: funkce 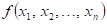 má v bodu má v bodu 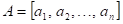 neostré lokální
maximum, právě když existuje takové okolí bodu neostré lokální
maximum, právě když existuje takové okolí bodu 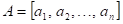 , že v něm platí , že v něm platí 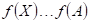 . .
|
|
|
35.
|
Doplňte
vhodné relační znaménko: funkce 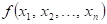 má v bodu má v bodu 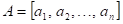 ostré lokální minimum,
právě když existuje takové okolí bodu ostré lokální minimum,
právě když existuje takové okolí bodu 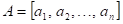 , že v něm platí , že v něm platí 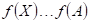 . .
|
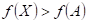
|
|
36.
|
Doplňte
vhodné relační znaménko: funkce 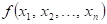 má v bodu má v bodu 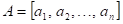 neostré lokální minimum,
právě když existuje takové okolí bodu neostré lokální minimum,
právě když existuje takové okolí bodu 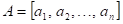 , že v něm platí , že v něm platí 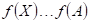 . .
|
|
|
37.
|
Dokončete
větu: má-li funkce 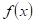 v bodu v bodu 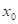 lokální extrém a
existuje-li derivace lokální extrém a
existuje-li derivace 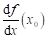 , potom , potom 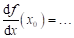
|
Má-li funkce 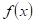 v bodu v bodu 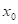 lokální extrém a
existují-li derivace lokální extrém a
existují-li derivace 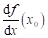 , potom , potom 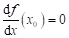 . .
|
|
38.
|
Dokončete
větu: má-li funkce 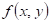 v bodu v bodu 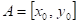 lokální extrém a
existují-li parciální derivace lokální extrém a
existují-li parciální derivace 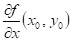 , , 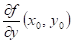 , potom , potom 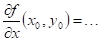 , , 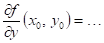
|
Má-li funkce 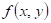 v bodu v bodu 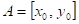 lokální extrém a
existují-li parciální derivace lokální extrém a
existují-li parciální derivace 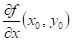 , , 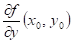 , potom , potom 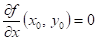 , , 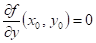 . .
|
|
39.
|
Dokončete
větu: má-li funkce 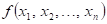 v bodu v bodu 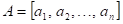 lokální extrém a
existují-li parciální derivace lokální extrém a
existují-li parciální derivace 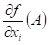 , , 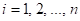 , potom , potom 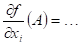
|
Má-li funkce 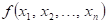 v bodu v bodu 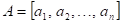 lokální extrém a
existují-li parciální derivace lokální extrém a
existují-li parciální derivace 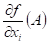 , , 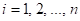 , potom , potom 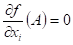
|