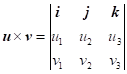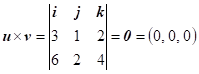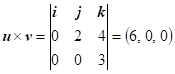Přednášky Zadání teoretických otázek a úkolů       Řešení teoretických otázek a úkolů       Vzorové řešené příklady Příklady na procvičení

1

1.1

1.2

1.3

1.4

1.5

1.6

1.6.1

1.6.2

1.6.3 Vektorový součin

Č.	Otázky	Odpovědi
1.	Jak značíme vektorový součin vektorů ?
2.	Co je výsledkem vektorového součinu  dvou nekolineárních vektorů?	Vektor, který je kolmý na vektory .
3.	Co je výsledkem vektorového součinu  dvou kolineárních vektorů?	Nulový vektor.
4.	Kdy je vektorový součin dvou vektorů roven nulovému vektoru?	Jestliže vektory jsou kolineární.
5.	Pro jaký úhel  dvou vektorů je jejich vektorový součin maximální?	Pro úhel .
6.	Pro jaký úhel  dvou vektorů je jejich vektorový součin roven nulovému vektoru?	Pro úhel .
7.	Co znamená, že vektorový součin  je antikomutativní?	Při záměně pořadí vektorů dojde ke změně znaménka vektorového součinu .
8.	Jak lze vypočítat velikost obsahu rovnoběžníku , známe-li souřadnice jeho vrcholů?	Sestrojíme vektory a . Vypočítáme jejich vektorový součin . Obsah rovnoběžníku  je pak číselně roven velikosti vektoru .
9.	Jak lze vypočítat velikost obsahu trojúhelníku , známe-li souřadnice jeho vrcholů?	Sestrojíme vektory a . Vypočítáme jejich vektorový součin . Obsah trojúhelníku  je pak číselně roven polovině velikosti vektoru .
10.	Co znamená, že vektory  následují v kladné orientaci?	Následují za sebou proti směru chodu hodinových ručiček podle pravidla pravé ruky.

Č.	Úkoly	Řešení úkolů
1.	Předpokládejme vektory , . Zapište formální vztah pro výpočet jejich vektorového součinu
2.	Zapište vztah pro výpočet velikosti vektorového součinu dvou nenulových vektorů  znáte-li jejich velikosti a úhel , který svírají.
3.	Z následujících výroků  a  vytvořte pravdivou ekvivalenci. Pokud by to nebylo možné, vytvořte pravdivou implikaci. : vektory  jsou kolineární, : vektorový součin .	Vektory  jsou kolineární, právě když jejich vektorový součin .
4.	Zapište vztah, který vyjadřuje antikomutativní vlastnost vektorového součinu
5.	Pro vektory  dopište distributivní zákon
6.	Pro vektory  a konstantu  odstraňte závorky ve výrazu
7.	Vypočítejte vektorový součin vektorů , .	, vektory jsou kolineární, 3. řádek je dvojnásobkem 2. řádku.
8.	Vypočítejte vektorový součin vektorů , .	, vektory nejsou kolineární. Při výpočtu determinantu v trojúhelníkovém tvaru pouze vynásobíme prvky na hlavní diagonále.