Přednášky        Zadání teoretických otázek a úkolů       Řešení teoretických otázek a úkolů       Vzorové řešené příklady            Příklady na procvičení

 

 

 

1      

1.1        

1.2        

1.3        

1.4        

1.5        

1.6        

1.6.1        

1.6.2        

1.6.3       Vektorový součin

Definice

Nechť  a  jsou libovolné vektory. Jejich vektorovým součinem je vektor, který je definován vztahem

.

Symbolický zápis:

.

 

 

 

 

 

 

 

Příklad

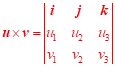Vypočítejte vektorový součin vektorů , .

 

 

 

 

 

Věta

Nechť  jsou vektory v bázi . Pak platí:

1.      právě tehdy, jsou-li  kolineární,

2.      … vektorový součin je antikomutativní,

3.     vektorový součin není asociativní,

4.      ... distributivní zákon,

5.     , kde .

 

 

 

 

 

Věta

Nechť  jsou nekolineární vektory. Vektorový součin  má tyto vlastnosti:

1.     je kolmý k oběma vektorům ,

2.     jeho velikost je číselně rovna obsahu rovnoběžníku sestrojeného z vektorů : ,  je úhel vektorů ,

3.     obsah trojúhelníku se stranami  je roven ,

4.     vektory v trojici   za sebou následují v kladné orientaci (proti směru chodu hodinových ručiček).

 

 

 

 

 

 

Příklad

Vypočítejte velikost obsahu rovnoběžníku, který je zadán vektory , .

 

 

 

Příklad z praxe

 

 Z fyziky víme, že moment  síly  vyjadřuje otáčivý účinek síly vzhledem k danému bodu prostoru a dané ose otáčení. Moment síly je vektor definovaný vektorovým součinem , kde  je vektor ramene sily.

Vypočítejte moment síly, který vyvolá cyklista sešlápnutím pedálu ve svislém směru silou velikosti , jestliže v okamžiku sešlápnutí svírá klika pedálu s vodorovnou základnou úhel . Délka kliky je .