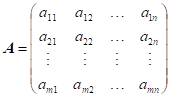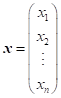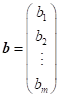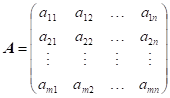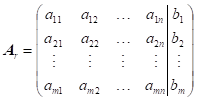1.4 Řešení soustav lineárních rovnic

Č.	Otázky	Odpovědi
1.	Co znamená, že dvě soustavy lineárních rovnic jsou ekvivalentní?	Mají stejná řešení.
2.	Jak se změní řešení soustavy lineárních rovnic, jestliže změníme pořadí rovnic?	Řešení se nezmění.
3.	Jak se změní řešení soustavy lineárních rovnic, jestliže libovolnou rovnici vynásobíme nenulovou konstantou?	Řešení se nezmění.
4.	Jak se změní řešení soustavy lineárních rovnic, jestliže vynecháme rovnici, která je lineární kombinací zbývajících rovnic?	Řešení se nezmění.
5.	Jak se změní řešení soustavy lineárních rovnic, jestliže přidáme rovnici, která je lineární kombinací zbývajících rovnic?	Řešení se nezmění.
6.	Jak se změní řešení soustavy lineárních rovnic, jestliže k jedné z rovnic přičteme lineární kombinaci zbývajících rovnic?	Řešení se nezmění.
7.	Jak se změní řešení soustavy lineárních rovnic, jestliže ekvivalentními úpravami soustavu upravíme na trojúhelníkový tvar?	Řešení se nezmění.
8.	Jak se změní hodnost matice soustavy lineárních rovnic po provedení ekvivalentních úprav?	Hodnost se nezmění.
9.	Co můžeme říci o řešitelnosti soustavy lineárních rovnic, jestliže hodnost matice soustavy je rovna hodnosti matice rozšířené?	Soustava má řešení, ale nevíme kolik těch řešení je.
10.	Co můžeme říci o řešitelnosti soustavy lineárních rovnic, jestliže hodnost matice soustavy je menší než hodnost matice rozšířené?	Soustava nemá řešení.
11.	Co můžeme říci o řešitelnosti soustavy lineárních rovnic, jestliže hodnost matice soustavy je rovna hodnosti matice rozšířené a zároveň je rovna počtu hledaných neznámých?	Soustava má jediné řešení.
12.	Co můžeme říci o řešitelnosti soustavy lineárních rovnic, jestliže hodnost matice soustavy je rovna hodnosti matice rozšířené a zároveň je menší než počet hledaných neznámých?	Soustava má nekonečně mnoho řešení s alespoň jedním volitelným parametrem.
13.	Předpokládejme, že soustava lineárních rovnic má nekonečně mnoho řešení. Jak určíme počet volitelných parametrů?	Počet volitelných parametrů je dán rozdílem mezi počtem hledaných neznámých a hodností matice soustavy.
14.	Co to je homogenní soustava lineárních rovnic?	Je to soustava s nulovým vektorem pravých stran.
15.	Co je to nehomogenní soustava lineárních rovnic?	Je to soustava s nenulovým vektorem pravých stran.
16.	Za jakých podmínek má homogenní soustava lineárních rovnic řešení?	Homogenní soustava lineárních rovnic má vždy řešení, a to triviální.
17.	Co to je triviální řešení homogenní soustavy lineárních rovnic?	Nulový sloupcový vektor neznámých.
18.	Za jakého předpokladu má homogenní soustava lineárních rovnic nekonečně mnoho řešení?	Jestliže počet hledaných neznámých je větší než hodnost matice soustavy.
19.	Jak nazýváme soustavu lineárních rovnic, která obsahuje stejný počet rovnic jako je počet neznámých?	Čtvercová soustava lineárních rovnic.
20.	Co to je čtvercová soustava lineárních rovnic?	Čtvercová soustava lineárních rovnic je taková soustava, která obsahuje stejný počet rovnic jako je počet neznámých.
21.	Co musí splňovat čtvercová soustava lineárních rovnic, aby měla právě jedno řešení?	Matice soustavy musí být regulární.
22.	Kolik řešení má nehomogenní čtvercová soustava lineárních rovnic s regulární maticí soustavy?	Právě jediné řešení.
23.	Za jakých podmínek lze použít Cramérovo pravidlo pro řešení soustav lineárních rovnic?	Soustava lineárních rovnic musí být čtvercová s regulární maticí soustavy.
24.	Kolik a jakých řešení má homogenní čtvercová soustava lineárních rovnic s regulární maticí?	Právě jediné, a to triviální řešení.
25.	Kolik a jakých řešení má homogenní čtvercová soustava lineárních rovnic se singulární maticí?	Soustava má nekonečně mnoho řešení s alespoň jedním parametrem, a to včetně triviálního řešení.

Č.	Úkoly	Řešení úkolů
1.	Předpokládejme matici soustavy lineárních rovnic , sloupcový vektor neznámých a sloupcový vektor pravých stran . Vytvořte maticový zápis soustavy lineárních rovnic.
2.	Předpokládejme matici soustavy lineárních rovnic a sloupcový vektor pravých stran . Vytvořte rozšířenou matici soustavy lineárních rovnic.
3.	Zapište alespoň dvě ekvivalentní úpravy soustavy lineárních rovnic.	Záměna pořadí dvou libovolných rovnic. Vynásobení libovolné rovnice nenulovou konstantou. Vynechání rovnice, která je lineární kombinací zbývajících rovnic. Přidání rovnice, která je lineární kombinací zbývajících rovnic. Přičtení lineární kombinace ostatních rovnic k jedné rovnici.
4.	Zapište vztah, pomocí kterého lze ze soustavy lineárních rovnic vypočítat hodnoty neznámých pomocí Cramérova pravidla.	pro je determinant při neznámé , který vznikne z determinantu soustavy tak, že sloupec koeficientů při neznámé nahradíme vektorem pravých stran. je determinant soustavy.