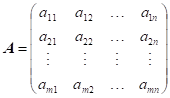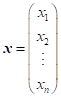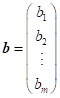Přednášky Zadání teoretických otázek a úkolů Řešení teoretických otázek a úkolů Vzorové řešené příklady Příklady na procvičení

1

1.1

1.2

1.3

1.4 Řešení soustav lineárních rovnic

Č.	Otázky
1.	Co znamená, že dvě soustavy lineárních rovnic jsou ekvivalentní?
2.	Jak se změní řešení soustavy lineárních rovnic, jestliže změníme pořadí rovnic?
3.	Jak se změní řešení soustavy lineárních rovnic, jestliže libovolnou rovnici vynásobíme nenulovou konstantou?
4.	Jak se změní řešení soustavy lineárních rovnic, jestliže vynecháme rovnici, která je lineární kombinací zbývajících rovnic?
5.	Jak se změní řešení soustavy lineárních rovnic, jestliže přidáme rovnici, která je lineární kombinací zbývajících rovnic?
6.	Jak se změní řešení soustavy lineárních rovnic, jestliže k jedné z rovnic přičteme lineární kombinaci zbývajících rovnic?
7.	Jak se změní řešení soustavy lineárních rovnic, jestliže ekvivalentními úpravami soustavu upravíme na trojúhelníkový tvar?
8.	Jak se změní hodnost matice soustavy lineárních rovnic po provedení ekvivalentních úprav?
9.	Co můžeme říci o řešitelnosti soustavy lineárních rovnic, jestliže hodnost matice soustavy je rovna hodnosti matice rozšířené?
10.	Co můžeme říci o řešitelnosti soustavy lineárních rovnic, jestliže hodnost matice soustavy je menší než hodnost matice rozšířené?
11.	Co můžeme říci o řešitelnosti soustavy lineárních rovnic, jestliže hodnost matice soustavy je rovna hodnosti matice rozšířené a zároveň je rovna počtu hledaných neznámých?
12.	Co můžeme říci o řešitelnosti soustavy lineárních rovnic, jestliže hodnost matice soustavy je rovna hodnosti matice rozšířené a zároveň je menší než počet hledaných neznámých?
13.	Předpokládejme, že soustava lineárních rovnic má nekonečně mnoho řešení. Jak určíme počet volitelných parametrů?
14.	Co to je homogenní soustava lineárních rovnic?
15.	Co je to nehomogenní soustava lineárních rovnic?
16.	Za jakých podmínek má homogenní soustava lineárních rovnic řešení?
17.	Co to je triviální řešení homogenní soustavy lineárních rovnic?
18.	Za jakého předpokladu má homogenní soustava lineárních rovnic nekonečně mnoho řešení?
19.	Jak nazýváme soustavu lineárních rovnic, která obsahuje stejný počet rovnic jako je počet neznámých?
20.	Co to je čtvercová soustava lineárních rovnic?
21.	Co musí splňovat čtvercová soustava lineárních rovnic, aby měla právě jedno řešení?
22.	Kolik řešení má nehomogenní čtvercová soustava lineárních rovnic s regulární maticí soustavy?
23.	Za jakých podmínek lze použít Cramérovo pravidlo pro řešení soustav lineárních rovnic?
24.	Kolik a jakých řešení má homogenní čtvercová soustava lineárních rovnic s regulární maticí?
25.	Kolik a jakých řešení má homogenní čtvercová soustava lineárních rovnic se singulární maticí?

Č.	Úkoly
1.	Předpokládejme matici soustavy lineárních rovnic , sloupcový vektor neznámých a sloupcový vektor pravých stran . Vytvořte maticový zápis soustavy lineárních rovnic.
2.	Předpokládejme matici soustavy lineárních rovnic a sloupcový vektor pravých stran . Vytvořte rozšířenou matici soustavy lineárních rovnic.
3.	Zapište alespoň dvě ekvivalentní úpravy soustavy lineárních rovnic.
4.	Zapište vztah, pomocí kterého lze ze soustavy lineárních rovnic vypočítat hodnoty neznámých pomocí Cramérova pravidla.