Přednášky Zadání teoretických otázek a úkolů Řešení teoretických otázek a úkolů Vzorové řešené příklady Příklady na procvičení
1.4 Řešení soustav lineárních rovnic
Příklad
Součet věku otce a syna je 50 roků. Otec je čtyřikrát starší než syn. Vypočítejte věk otce a věk syna.
Předpokládejme soustavu ![]() lineárních rovnic o
lineárních rovnic o ![]() neznámých
neznámých ![]() , kterou lze zapsat
ve tvaru:
, kterou lze zapsat
ve tvaru:
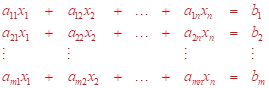
Matice soustavy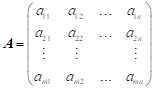 je maticí
koeficientů při neznámých. Pro
je maticí
koeficientů při neznámých. Pro ![]() nazýváme
soustavu čtvercovou.
nazýváme
soustavu čtvercovou.
Sloupcový
vektor pravých stran 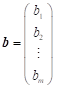 .
.
Rozšířená
matice soustavy 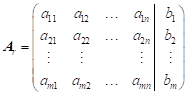 .
.
Sloupcový
vektor neznámých 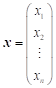 .
.
Maticový zápis
soustavy lineárních rovnic ![]() .
.
Dvě soustavy rovnic jsou ekvivalentní právě tehdy, když mají stejnou množinu řešení.
Z výchozí soustavy lze získat soustavu ekvivalentní těmito ekvivalentními úpravami:
· záměnou pořadí dvou libovolných rovnic soustavy,
· vynásobením libovolné rovnice soustavy nenulovou konstantou,
· vynecháním nebo připojením nulové rovnice, nebo rovnice, která je lineární kombinací ostatních rovnic soustavy,
· přičtením lineární kombinace ostatních rovnic k dané rovnici soustavy.
Uvedenými úpravami se nezmění hodnost matice soustavy ani hodnost rozšířené matice soustavy.
Pro nalezení řešení soustavy lineárních rovnic upravíme rozšířenou matici soustavy na trojúhelníkový tvar pomocí ekvivalentních úprav.
Soustava
![]() lineárních rovnic
o
lineárních rovnic
o ![]() neznámých je řešitelná právě tehdy, když hodnost matice soustavy je rovna hodnosti matice
rozšířené.
neznámých je řešitelná právě tehdy, když hodnost matice soustavy je rovna hodnosti matice
rozšířené.
Jestliže společná hodnost
matice soustavy a matice rozšířené je
menší než počet neznámých: ![]() , pak má soustava lineárních rovnic
, pak má soustava lineárních rovnic ![]() nekonečně mnoho řešení. Hodnota rozdílu
nekonečně mnoho řešení. Hodnota rozdílu ![]() je rovna počtu volitelných neznámých (parametrů) v soustavě. Parametrické neznámé je třeba
volit tak, aby sloupcové vektory
je rovna počtu volitelných neznámých (parametrů) v soustavě. Parametrické neznámé je třeba
volit tak, aby sloupcové vektory 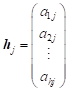 koeficientů
zbývajících neznámých byly vzájemně lineárně nezávislé.
koeficientů
zbývajících neznámých byly vzájemně lineárně nezávislé.
Je-li vektor pravých stran ![]() nulový,
nazýváme soustavu rovnic homogenní,
v ostatních případech nehomogenní.
nulový,
nazýváme soustavu rovnic homogenní,
v ostatních případech nehomogenní.
Homogenní soustava rovnic má vždy řešení. Nulový vektor je řešením každé homogenní soustavy rovnic.
Čtvercová
soustava lineárních rovnic má stejný počet rovnic jako neznámých a
má jediné řešení právě tehdy,
když je matice soustavy ![]() regulární.
regulární.
Homogenní
čtvercová soustava s regulární maticí má jediné tzv. triviální řešení 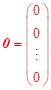 .
.
Vypočítejte řešení soustavy lineárních rovnic 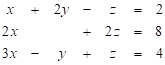 .
.
Vypočítejte řešení soustavy lineárních rovnic o
třech neznámých, jestliže po úpravě na trojúhelníkový tvar jsme získali
rozšířenou matici soustavy ve tvaru ![]() .
.
Vypočítejte řešení soustavy lineárních rovnic o
třech neznámých, jestliže po úpravě na trojúhelníkový tvar jsme získali
rozšířenou matici soustavy ve tvaru 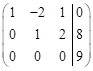 .
.
Vypočítejte řešení soustavy lineárních rovnic o
třech neznámých, jestliže po úpravě na trojúhelníkový tvar jsme získali
rozšířenou matici soustavy ve tvaru 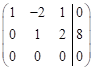 .
.
Vypočítejte řešení soustavy lineárních rovnic o
třech neznámých, jestliže po úpravě na trojúhelníkový tvar jsme získali
rozšířenou matici soustavy ve tvaru 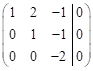 .
.
Věta
Řešení čtvercové
soustavy lineárních rovnic s regulární
maticí soustavy ![]() lze
určit podle vztahu
lze
určit podle vztahu
![]() pro
pro ![]() ,
,
kde ![]() je tzv. determinant soustavy,
je tzv. determinant soustavy,
![]() jsou tzv. determinanty při neznámých, které vzniknou
z determinantu soustavy tak, že v něm sloupec koeficientů při neznámé
jsou tzv. determinanty při neznámých, které vzniknou
z determinantu soustavy tak, že v něm sloupec koeficientů při neznámé
![]() nahradíme sloupcem
pravých stran soustavy.
nahradíme sloupcem
pravých stran soustavy.
Příklad
Pomocí Cramerova pravidla vypočítejte řešení
soustavy lineárních rovnic ![]() .
.
Příklad z praxe
 V současnosti nejpoužívanějším pojivem ve stavebnictví jsou
cementy, a to především portlandský cement. Vyrábí se vypalováním směsi surovin
za vzniku portlandského slínku, který se následně mele s dalšími
přísadami. Základními surovinami jsou vápenec, jíl, křemen a železná ruda.
V následující tabulce je uvedeno procentuální zastoupení CaO, SiO2,
Al2O3 a Fe2O3 v daných
surovinách. Jaké procentuální zastoupení uvedených surovin musíme použít, aby
výsledný portlandský cement obsahoval 66,0 % CaO, 23,3 % SiO2, 6,7 %
Al2O3 a 4,0 % Fe2O3?
V současnosti nejpoužívanějším pojivem ve stavebnictví jsou
cementy, a to především portlandský cement. Vyrábí se vypalováním směsi surovin
za vzniku portlandského slínku, který se následně mele s dalšími
přísadami. Základními surovinami jsou vápenec, jíl, křemen a železná ruda.
V následující tabulce je uvedeno procentuální zastoupení CaO, SiO2,
Al2O3 a Fe2O3 v daných
surovinách. Jaké procentuální zastoupení uvedených surovin musíme použít, aby
výsledný portlandský cement obsahoval 66,0 % CaO, 23,3 % SiO2, 6,7 %
Al2O3 a 4,0 % Fe2O3?
|
CaO |
SiO2 |
Al2O3 |
Fe2O3 |
|
|
vápenec |
76 |
15 |
5 |
4 |
|
jíl |
2 |
44 |
51 |
3 |
|
křemen |
1 |
96 |
1 |
2 |
|
železná ruda |
1 |
12 |
9 |
78 |