Přednášky Zadání teoretických otázek a úkolů Řešení teoretických otázek a úkolů Vzorové řešené příklady Příklady na procvičení
5.4.2 Vlastnosti Riemannových integrálů
Věta
Jestliže mají funkce ![]() ,
, ![]() Riemannův
integrál na intervalu
Riemannův
integrál na intervalu ![]() , pak platí následující vztahy.
, pak platí následující vztahy.
Linearita 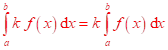 ; kde konstanta
; kde konstanta ![]()
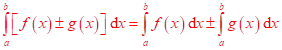
Monotonie ![]() ;
;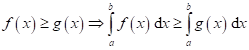
(speciálně
pro 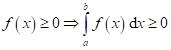 )
)
Absolutní
konvergence 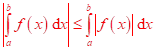
Aditivnost 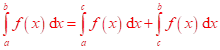 ;
; ![]() ,
, ![]()
Odhad
integrálu ![]() :
:
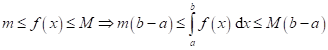
Záměna
mezí 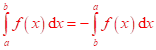
Věta: O střední hodnotě integrálního počtu
Má-li funkce ![]() na intervalu
na intervalu ![]() Riemannův
integrál, přičemž
Riemannův
integrál, přičemž
![]() :
: ![]() ,
,
pak existuje takové ![]() , zvané střední hodnota funkce
, zvané střední hodnota funkce ![]() na
intervalu
na
intervalu ![]() , že
, že
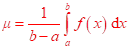
Pro ![]() je
je
![]() ,
, ![]()
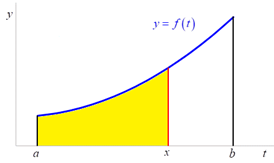
Věta
Funkce ![]() horní
meze
horní
meze ![]() ,
, ![]() definovaná
vztahem
definovaná
vztahem
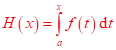
je spojitá na intervalu ![]() , na němž existuje Riemannův integrál
funkce
, na němž existuje Riemannův integrál
funkce ![]() .
.
Věta: Newtonova – Leibnizova. Základní věta integrálního počtu.
Je-li funkce ![]() a
a ![]() je
na intervalu
je
na intervalu ![]() její primitivní funkce, pak
Riemannův integrál
její primitivní funkce, pak
Riemannův integrál
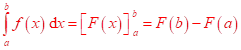
Věta platí i pro případ, kdy
funkce ![]() na
na ![]() má konečný počet bodů nespojitosti
prvního druhu.
má konečný počet bodů nespojitosti
prvního druhu.
·
Vypočítejte ![]()
·
Vypočítejte ![]()
Příklad z praxe
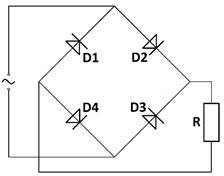 Časový
průběh usměrněného napětí na výstupu dvoucestného usměrňovače lze popsat
rovnicí
Časový
průběh usměrněného napětí na výstupu dvoucestného usměrňovače lze popsat
rovnicí ![]() .
.
Vypočítejte střední hodnotu ![]() stejnosměrného napětí na výstupu
dvoucestného usměrňovače, jestliže na jeho vstup je přiváděno střídavé napětí
s maximální hodnotou
stejnosměrného napětí na výstupu
dvoucestného usměrňovače, jestliže na jeho vstup je přiváděno střídavé napětí
s maximální hodnotou ![]() a
s frekvencí
a
s frekvencí ![]() .
Načrtněte graf závislosti jak vstupního střídavého, tak i výstupního
stejnosměrného napětí usměrňovače na čase
.
Načrtněte graf závislosti jak vstupního střídavého, tak i výstupního
stejnosměrného napětí usměrňovače na čase ![]() . Do grafu s výstupním napětím
vyneste vypočtenou střední hodnotu
. Do grafu s výstupním napětím
vyneste vypočtenou střední hodnotu ![]() výstupního
napětí.
výstupního
napětí.
Příklad z praxe
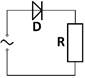 Časový
průběh usměrněného napětí na výstupu jednocestného usměrňovače lze popsat
rovnicí:
Časový
průběh usměrněného napětí na výstupu jednocestného usměrňovače lze popsat
rovnicí:
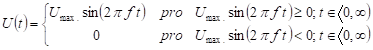 Načrtněte
graf závislosti jak vstupního střídavého, tak i výstupního stejnosměrného
napětí jednocestného usměrňovače na čase
Načrtněte
graf závislosti jak vstupního střídavého, tak i výstupního stejnosměrného
napětí jednocestného usměrňovače na čase ![]() , jestliže na jeho vstup je přiváděno
střídavé napětí s maximální hodnotou
, jestliže na jeho vstup je přiváděno
střídavé napětí s maximální hodnotou ![]() a s frekvencí
a s frekvencí ![]() . Vypočítejte střední
hodnotu
. Vypočítejte střední
hodnotu ![]() stejnosměrného
napětí na výstupu usměrňovače a tuto hodnotu vyneste do grafu s výstupním
napětím.
stejnosměrného
napětí na výstupu usměrňovače a tuto hodnotu vyneste do grafu s výstupním
napětím.
Příklad z praxe
 Efektivní
hodnota střídavého proudu/napětí je rovna hodnotě proudu/napětí stejnosměrného,
který v daném obvodu vykoná za stejný čas stejnou práci jako proud/napětí
střídavý. V elektrickém obvodu s konstantním stejnosměrným
proudem/napětím je možno práci
Efektivní
hodnota střídavého proudu/napětí je rovna hodnotě proudu/napětí stejnosměrného,
který v daném obvodu vykoná za stejný čas stejnou práci jako proud/napětí
střídavý. V elektrickém obvodu s konstantním stejnosměrným
proudem/napětím je možno práci ![]() vykonanou
za čas
vykonanou
za čas ![]() vypočítat
ze součinu
vypočítat
ze součinu ![]() , kde výkon
, kde výkon ![]() je dán součinem
napětí
je dán součinem
napětí ![]() a proudu
a proudu ![]() , tedy
, tedy ![]() při současné platnosti
Ohmova zákona
při současné platnosti
Ohmova zákona ![]() .
V elektrickém obvodu se střídavým proudem/napětím je okamžitá hodnota
výkonu dána vztahem
.
V elektrickém obvodu se střídavým proudem/napětím je okamžitá hodnota
výkonu dána vztahem ![]() .
Časový průběh střídavého proudu lze popsat rovnicí
.
Časový průběh střídavého proudu lze popsat rovnicí ![]() , kde
, kde ![]() je maximální hodnota střídavého
proudu.
je maximální hodnota střídavého
proudu.
Vypočítejte efektivní hodnotu střídavého proudu, jestliže
maximální hodnota střídavého proudu je ![]() . Obdobně vypočítejte efektivní
hodnotu střídavého napětí, jestliže maximální hodnota střídavého napětí
. Obdobně vypočítejte efektivní
hodnotu střídavého napětí, jestliže maximální hodnota střídavého napětí ![]() .
.