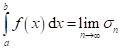Přednášky          Zadání teoretických otázek a úkolů Řešení teoretických otázek a úkolů

5.4 Určitý integrál

5.4.1 Riemannův určitý integrál

Důležité pojmy

Dělení  intervalu , kde , je množina dělicích bodů

Element délky

Norma dělení intervalu

,             

Volbou  vznikne na intervalu posloupnost dělení  a s ní posloupnost norem dělení .

Normální posloupnosti dělení jsou takové, pro které platí

Nejmenší a největší hodnota funkce

,               ,            

,              ,            

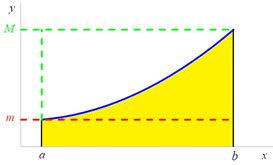
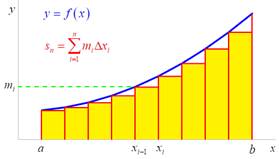
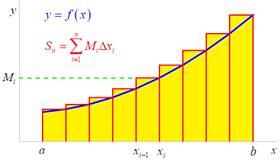
Odhad obsahu  obrazce pomocí obsahů „vepsaného“ a „opsaného“ obdélníka

Minimální a maximální element obsahu

,                

Dolní a horní integrální součet

,               

Pro libovolné normální posloupnosti dělení  platí:

• posloupnost 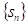 je neklesající a shora omezená číslem

• posloupnost 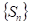 je nerostoucí a zdola omezená číslem

Definice

Právě když pro libovolnou normální posloupnost dělení  intervalu  mají příslušné posloupnosti dolních součtů  a horních součtů  funkce  tutéž vlastní limitu

,

nazýváme toto číslo Riemannovým určitým integrálem funkce  od  do . Označujeme je

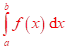
Věta: Postačující podmínka integrability

Jestliže funkce , pak existuje Riemannův integrál .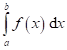

Obecnější podmínka integrability: funkce  je na intervalu po částech spojitá. To znamená, že funkce je ohraničená.

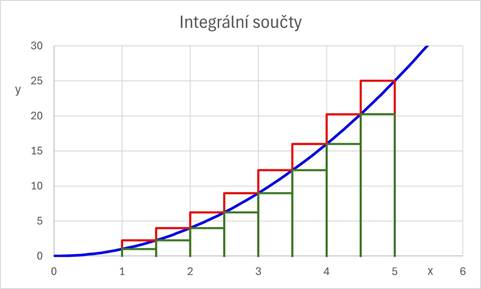
Posloupnost integrálních součtů:

,  příslušných k posloupnosti dělení , jejichž

Věta

Má-li funkce  na intervalu  Riemannův určitý integrál, pak pro normální posloupnost dělení  je