Přednášky Zadání teoretických otázek a úkolů Řešení teoretických otázek a úkolů Vzorové řešené příklady Příklady na procvičení

4.4 Taylorův polynom a jeho užití

Předpokládejme, že funkce má v bodu derivace a hledejme polynom nejvýš stupně ve tvaru

.

Koeficienty náhradního polynomu určeme tak, aby měl stejnou funkční hodnotu a stejné hodnoty derivací v bodu , jako má v tomto bodu funkce .

Taylorův polynom (nejvýše) stupně funkce v bodu :

Příklad

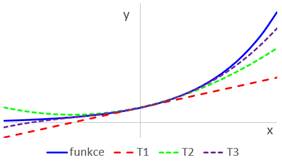
Sestavte Taylorův polynom 3. stupně pro funkci v bodu .

Věta Taylorova

Nechť je funkce v okolí daného bodu , je libovolný bod tohoto okolí, . Pak existuje bod takový, že platí (Taylorův vzorec):

kde (Lagrangeův tvar zbytku)

,

bod je mezi body a .

Příklad

Sestavte Taylorův polynom 3. stupně pro funkci v bodě . Vypočítejte hodnotu a odhadněte velikost zbytku.

Taylorův vzorec pro bývá označován jako Maclaurinův vzorec.

Důsledky Taylorovy věty

Taylorova věta pro

Lagrangeova věta o střední hodnotě diferenciálního počtu (věta o přírůstku funkce)

Jestliže v okolí bodu a je bod tohoto okolí, pak

, je mezi , .

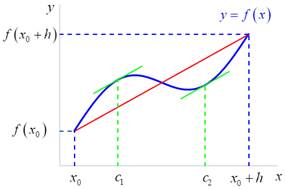
Přírůstek funkce

, je mezi ,

Rolleova věta

Jestliže v okolí bodu , obsahujícím bod a jestliže , pak existuje alespoň jeden bod mezi , takový, že .

Taylorova věta pro

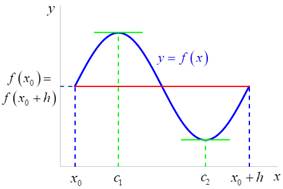
Jestliže v okolí bodu a je bod tohoto okolí, pak

, je mezi , .

Přírůstek funkce

, je mezi ,

Přibližné výpočty a odhady

Přírůstek funkce

Funkční hodnota

Absolutní chyba

Relativní chyba

Procentuální chyba

Taylorův vzorec s využitím diferenciálů

Příklad

Vypočítejte hodnotu diference, diferenciálu a pomocí diferenciálu odhadněte hodnotu absolutní chyby, relativní chyby a procentuální chyby funkce v bodu a pro přírůstek nezávisle proměnné .