Přednášky          Zadání teoretických otázek a úkolů         Řešení teoretických otázek a úkolů         Vzorové řešené příklady               Příklady na procvičení

 

 

 

3.2.8 Racionální funkce

Polynom je funkce s reálnými koeficienty :

pro  je stupeň polynomu právě .

Kořenem polynomu rozumíme takové číslo  (reálné nebo komplexní), pro něž .

 

Věta: Základní věta algebry

Každý polynom alespoň 1. stupně má v oboru komplexních čísel alespoň jeden kořen.

 

Bézoutova věta

Číslo  je kořenem polynomu  stupně alespoň prvního (), právě když , kde  je polynom stupně .

 

D´ Alembertova věta

Polynom  má v oboru komplexních čísel právě  kořenů, přičemž každý  násobný kořen počítáme za  kořenů.

 

Rozklad polynomu

Každý polynom je v oboru reálných čísel jednoznačně rozložitelný na součin koeficientu , reálných kořenových činitelů , které odpovídají reálným kořenům , a kvadratických trojčlenů ; , které odpovídají dvojicím komplexně sdružených kořenů.

 

 

 

Příklad

Polynom  rozložte na součin kořenových činitelů.

 

 

 

Racionální lomená funkce

 

Pro  rozlišujeme:

          ryze lomená racionální funkce

  neryze lomená racionální funkce

 

Neryze lomené racionální funkce rozkládáme na součet celistvé funkce a racionální ryze lomené funkce.

 

 

 

Příklad

Rozložte neryze lomenou racionální funkci  na součet celistvé funkce a racionální ryze lomené funkce.

 

 

 

Ryze lomené racionální funkce rozkládáme na součet parciálních (částečných) zlomků.

Parciální zlomky             

 

, , ,

, tj. trojčlen  je nerozložitelný v oboru reálných čísel.

 

Věta: O rozkladu ryze lomené racionální funkce

Jestliže jmenovatel  ryze lomené racionální funkce  má v reálném oboru rozklad

přičemž , , pak lze danou ryze lomenou racionální funkci jednoznačně rozložit na součet parciálních zlomků, kde

• každému 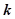 násobnému reálnému kořenu 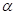 v rozkladu přísluší 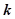 sčítanců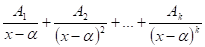

 

• každému  násobnému komplexnímu kořenu  (spolu s h násobným ) v rozkladu přísluší  sčítanců , v nichž .

 

 

Koeficienty  jsou reálná čísla, jejichž celkový počet je týž jako stupeň polynomu .

 

 

 

Příklad

Rozložte racionální ryze lomenou funkci  na součet parciálních zlomků.

 

 

 

Příklad

Rozložte racionální ryze lomenou funkci  na součet parciálních zlomků.

 

 

 

Příklady

Navrhněte tvary parciálních zlomků pro rozklady racionálních ryze lomených funkcí: ; ;  na součet parciálních zlomků.