Přednášky          Zadání teoretických otázek a úkolů Řešení teoretických otázek a úkolů Vzorové řešené příklady Příklady na procvičení

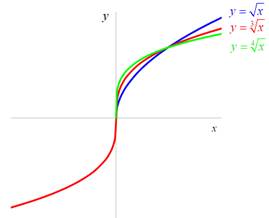
3.2.2 Mocninné funkce

 (reálný exponent), definiční obor závisí na hodnotě exponentu

 (přirozený exponent), definiční obor:

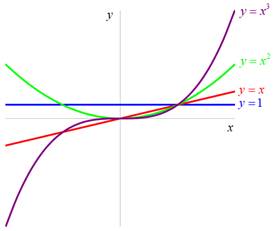
, (grafem je přímka, přímá úměrnost)

, (grafem je parabola)

, (grafem je kubická parabola)

, pro liché : , pro sudé :

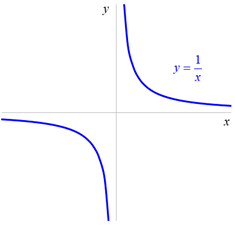
, (grafem je rovnoosá hyperbola, nepřímá úměrnost)

Rovnice přímky se směrnicí  a úsekem  na ose :

Rovnice přímky se směrnicí , která prochází bodem

Příklad z praxe

Plavební komora na Labi v Pardubicích má rozměry: délka , šířka . Výška hladiny Labe pod zdymadlem je , nominální vzdutá hladina je s povolenou tolerancí . Předpokládejme vzdutou hladinu  Dále předpokládejme, že komora bude napouštěna vodou s přítokem .

Sestavte funkci, která bude popisovat závislost výšky hladiny na čase během napouštění komory. Za jak dlouho se komora zcela zaplní vodou? Vypočtený čas vyjádřete v minutách a sekundách. Funkční závislost znázorněte graficky. S ohledem na fyzikální podstatu úlohy stanovte definiční obor a obor hodnot vytvořené funkce.

Příklad z praxe

Při rovnoměrně zrychleném pohybu hmotného bodu lze závislost rychlosti  a dráhy  bodu na čase  popsat rovnicemi: , , kde  je rychlost hmotného bodu na začátku pohybu v čase ,  je dráha hmotného bodu na začátku pohybu v čase ,  je zrychlení, resp. zpomalení pohybu.

Předpokládejme, že automobil se z klidového stavu začne rozjíždět rovnoměrně zrychleným pohybem se zrychlením .

Vypočítejte, jakou rychlostí se bude automobil pohybovat v čase  a jakou dráhu za tento čas ujede. Rychlost vyjádřete v . Sestavte funkce, které popisují závislosti rychlosti  resp. dráhy  automobilu na čase . Závislosti rychlosti automobilu a ujeté dráhy na čase znázorněte graficky.

Příklad z praxe

Předpokládejme vlak, který po minutě jízdy stálou rychlostí  začne brzdit rovnoměrně zpomaleným pohybem se zpomalením , až zastaví.

Sestavte funkce, které popisují závislosti rychlosti resp. dráhy vlaku na čase. Závislosti rychlosti  vlaku a ujeté dráhy  na čase  znázorněte graficky. Vypočítejte, jak dlouho bude vlak brzdit a jakou vzdálenost za tuto dobu ujede.

Příklad z praxe

Parašutista, který vyskočí z letadla, v prvé fázi letí volným pádem a v následující fázi letí na padáku. Pro popis jeho letu v obou fázích lze použít pohybovou rovnici , kde  je výsledná síla působící na parašutistu během jeho letu,  je síla způsobená tíhovým zrychlením a  je síla způsobená odporem vzduchu. Pro turbulentní proudění vzduchu pak po dosazení získáváme pohybovou rovnici v obecném tvaru , kde  je hmotnost padajícího tělesa,  je zrychlení pohybu tělesa, je tíhové zrychlení,  je součinitel odporu tělesa,  je průřez tělesa,  je hustota vzduchu,  je rychlost padajícího tělesa.

Vyjádřete závislost zrychlení  na rychlosti  padajícího tělesa. Co o této funkci můžete říci z hlediska monotónnosti a ohraničenosti? V obou fázích letu parašutisty postupně dojde k vyrovnání proti sobě působících sil  a , takže rovnoměrně zrychlený resp. zpomalený pohyb přechází do pohybu rovnoměrného. Vyjádřete vztah pro výpočet mezní rychlosti padajícího tělesa. Pro hodnoty , ,  vypočítejte mezní rychlost parašutisty ve fázi volného pádu pro ,  a ve fázi letu na padáku pro , . Pro obě fáze letu parašutisty stanovte definiční obory a obory hodnot závislosti zrychlení na rychlosti, a to s ohledem na fyzikální smysl dané úlohy.

Příklad z praxe

Předpokládejme izotermický děj. To znamená, že teplota  zůstává konstantní. Pak pro ideální plyn platí Boyleův – Mariottův zákon: , kde  je tlak plynu a  je objem plynu. Předpokládáme-li izotermický děj s výchozími hodnotami tlaku a objemu plynu  a koncovými hodnotami , pak lze uvedený zákon psát ve tvaru .

Zapište funkční vztah pro závislost tlaku  na objemu  plynu. Tuto funkční závislost znázorněte graficky. Jak se změní tlak plynu, jestliže jeho objem zmenšíme na  původního objemu? Objem pneumatiky nákladního automobilu je přibližně . Kolik litrů vzduchu při atmosférickém tlaku  je třeba stlačit, aby tlak vzduchu uvnitř pneumatiky byl ?