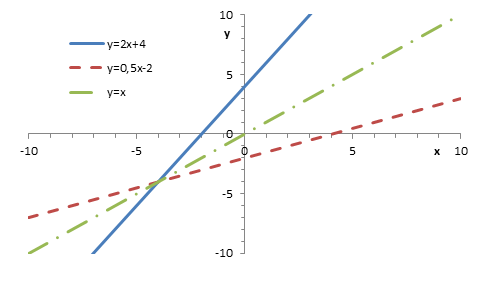3 Funkce a její limita

Č.

Otázky

Odpovědi

1. 

Předpokládejme neprázdnou množinu . Jak nazýváme zobrazení , kde každému  jediné ?

Reálná funkce jedné reálné proměnné.

2. 

Předpokládejme neprázdnou množinu  a zobrazení , kde každému  jediné . Co rozumíme definičním oborem tohoto zobrazení?

Definičním oborem je množina vzorů .

3. 

Předpokládejme neprázdnou množinu  a zobrazení , kde každému  jediné . Co rozumíme oborem (funkčních) hodnot tohoto zobrazení?

Oborem funkčních hodnot je množina obrazů .

4. 

Předpokládejme reálnou funkci jedné reálné proměnné. Co značíme zápisem ?

Definiční obor funkce .

5. 

Předpokládejme reálnou funkci jedné reálné proměnné. Co značíme zápisem ?

Obor funkčních hodnot funkce .

6. 

Předpokládejme reálnou funkci jedné reálné proměnné, . Jak nazýváme proměnné  a ?

 je nezávisle proměnná (argument)

 je závisle proměnná

7. 

Kdy považujeme dvě funkce za sobě rovné?

Dvě funkce považujeme za sobě rovné tehdy a jen tehdy, mají-li týž definiční obor a přiřazují-li obě ke každému  z definičního oboru totéž  z oboru hodnot.

8. 

Co rozumíme grafem funkce  jedné reálné proměnné?

Grafem funkce  jedné reálné proměnné rozumíme množinu bodů , , .

9. 

O jakou funkci  (z hlediska růstu a klesání), která je definovaná na množině , se jedná, jestliže platí ?

Rostoucí funkce.

10. 

O jakou funkci  (z hlediska růstu a klesání), která je definovaná na množině , se jedná, jestliže platí ?

Nerostoucí funkce.

11. 

O jakou funkci  (z hlediska růstu a klesání), která je definovaná na množině , se jedná, jestliže platí ?

Klesající funkce.

12. 

O jakou funkci  (z hlediska růstu a klesání), která je definovaná na množině , se jedná, jestliže platí ?

Neklesající funkce.

13. 

Jak souhrnně nazýváme rostoucí, klesající, nerostoucí a neklesající funkce?

Monotónní funkce.

14. 

Jak souhrnně nazýváme rostoucí a klesající funkce?

Ryze monotónní funkce.

15. 

Které typy funkcí řadíme mezi monotónní funkce?

Rostoucí, klesající, nerostoucí a neklesající funkce.

16. 

Které typy funkcí řadíme mezi ryze monotónní funkce?

Rostoucí a klesající funkce.

17. 

Co můžeme říci o funkci , která je definovaná na množině , jestliže platí ?

Funkce je shora omezená (ohraničená).

18. 

Co můžeme říci o funkci , která je definovaná na množině , jestliže platí ?

Funkce je zdola omezená (ohraničená).

19. 

Co můžeme říci o funkci , která je definovaná na množině , jestliže platí ?

Funkce je omezená (ohraničená).

20. 

Co můžeme říci o funkci , která je definovaná na množině , jestliže platí ?

Funkce je prostá.

21. 

Předpokládejme funkci  s definičním oborem  a s oborem hodnot . Jak nazveme funkci  definovanou na oboru , pro kterou platí ?

Funkci  nazýváme inverzní funkcí k funkci .

22. 

Jaký předpoklad musí splňovat funkce , aby k ní existovala inverzní funkce ?

Funkce  musí být prostá.

23. 

Jak postupujeme při sestavování inverzních funkcí?

Z funkce  vyjádříme proměnnou  jako funkci proměnné , tj.  a provedeme formální záměnu označení proměnných .

24. 

Jaký je vztah mezi definičním oborem , oborem funkčních hodnot  funkce  a definičním oborem , oborem funkčních hodnot  k ní inverzní funkce ?

25. 

Jaký je vztah mezi grafem funkce  a grafem k ní inverzní funkce  po záměně proměnných?

Grafy vzájemně inverzních funkcí  a  jsou po záměně proměnných souměrně sdružené podle přímky , tj. podle osy 1. a 3. kvadrantu.

26. 

Co můžeme říci o funkci , která je definovaná na množině , jestliže platí ?

Funkce  je sudá.

27. 

Co můžeme říci o funkci , která je definovaná na množině , jestliže platí ?

Funkce  je lichá.

28. 

Jak je souměrný graf sudé funkce?

Graf sudé funkce je souměrný podle osy .

29. 

Jak je souměrný graf liché funkce?

Graf liché funkce je souměrný podle počátku souřadného systému.

30. 

Co můžeme říci o funkci , která je definovaná na množině , jestliže platí ?

Funkce  je periodická.

31. 

Předpokládejme funkci, pro kterou platí ? Co vyjadřuje parametr ?

Parametr  vyjadřuje periodu periodické funkce.

32. 

Předpokládejme funkci , , . Jak nazýváme jednotlivé funkce, které jsou označeny písmeny ,  a ?

 = složená funkce

 = vnější funkce

 = vnitřní funkce

Č.

Úkoly

Řešení úkolů

1. 

Pro funkci  vypočítejte funkční hodnoty , .

2. 

Pro funkci  vypočítejte funkční hodnoty , .

3. 

Pro funkci  vypočítejte funkční hodnoty , .

4. 

Z následujících výroků  a  vytvořte pravdivou ekvivalenci. Pokud by to nebylo možné, vytvořte pravdivou implikaci.

: dvě funkce považujeme za sobě rovné,

: dvě funkce mají týž definiční obor a obě přiřazují ke každému  z definičního oboru totéž  z oboru hodnot.

Dvě funkce považujeme za sobě rovné tehdy a jen tehdy, mají-li týž definiční obor a přiřazují-li obě ke každému  z definičního oboru totéž  z oboru hodnot.

5. 

Z následujících výroků  a  vytvořte pravdivou ekvivalenci. Pokud by to nebylo možné, vytvořte pravdivou implikaci.

 funkce je monotónní,

 funkce je ryze monotónní.

Jestliže je funkce ryze monotónní, pak je monotónní.

6. 

Určete definiční obor a obor hodnot funkce , která je inverzní k funkci , pro kterou platí: .

7. 

Určete definiční obor a obor hodnot funkce , která je inverzní k funkci , pro kterou platí: .

8. 

Určete definiční obor a obor hodnot funkce , která je inverzní k funkci , pro kterou platí: .

9. 

K funkci  určete inverzní funkci , definiční obor  a obor hodnot  této inverzní funkce.

, ,

10. 

K funkci  určete inverzní funkci , definiční obor  a obor hodnot  této inverzní funkce.

, ,

11. 

K funkci  určete inverzní funkci , definiční obor  a obor hodnot  této inverzní funkce.

, ,

12. 

K funkci  určete inverzní funkci , definiční obor  a obor hodnot  této inverzní funkce.

, ,

13. 

K funkci  určete inverzní funkci , definiční obor  a obor hodnot  této inverzní funkce.

, ,

14. 

K funkci  určete inverzní funkci , definiční obor  a obor hodnot  této inverzní funkce.

, ,

15. 

K funkci  určete inverzní funkci , definiční obor  a obor hodnot  této inverzní funkce.

, ,

16. 

K funkci  určete inverzní funkci , definiční obor  a obor hodnot  této inverzní funkce.

, ,

17. 

K funkci  určete inverzní funkci , definiční obor  a obor hodnot  této inverzní funkce.

, ,

18. 

K funkci  určete inverzní funkci , definiční obor  a obor hodnot  této inverzní funkce.

, ,

19. 

K funkci  určete inverzní funkci , definiční obor  a obor hodnot  této inverzní funkce.

, ,

20. 

K funkci  určete inverzní funkci , definiční obor  a obor hodnot  této inverzní funkce.

, ,

21. 

K funkci  určete inverzní funkci , definiční obor  a obor hodnot  této inverzní funkce.

, ,

22. 

K funkci  určete inverzní funkci , definiční obor  a obor hodnot  této inverzní funkce.

, ,

23. 

Načrtněte grafy vzájemně inverzních funkcí ,  a osu 1. a 3. kvadrantu.

24. 

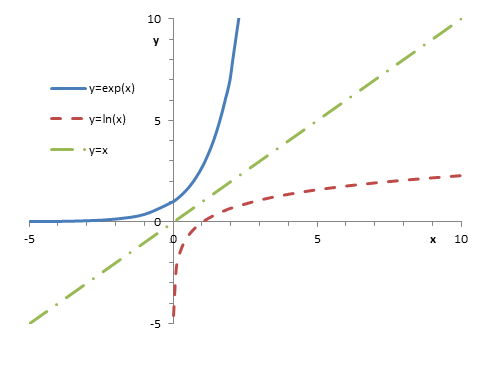
Načrtněte grafy vzájemně inverzních funkcí ,  a osu 1. a 3. kvadrantu.

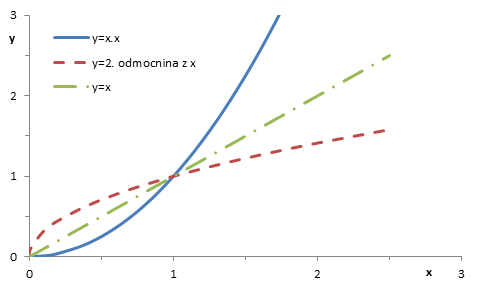
25. 

Načrtněte grafy vzájemně inverzních funkcí ,  a osu 1. a 3. kvadrantu pro .

26. 

Předpokládejme dva výroky platné pro funkci , která je definovaná na množině . Z následujících výroků  a  vytvořte pravdivou ekvivalenci. Pokud by to nebylo možné, vytvořte pravdivou implikaci.

 funkce  je sudá,

 .

Funkce  je sudá právě když .

27. 

Předpokládejme dva výroky platné pro funkci , která je definovaná na množině . Z následujících výroků  a  vytvořte pravdivou ekvivalenci. Pokud by to nebylo možné, vytvořte pravdivou implikaci.

 funkce  je lichá

 .

Funkce  je lichá právě když .

28. 

Předpokládejme dva výroky platné pro funkci , která je definovaná na množině . Z následujících výroků  a  vytvořte pravdivou ekvivalenci. Pokud by to nebylo možné, vytvořte pravdivou implikaci.

 funkce  je periodická s periodou ,

 .

Funkce  je periodická s periodou  právě když .

29. 

Složenou funkci  rozepište pomocí vnější a vnitřní funkce.

Vnější funkce: , vnitřní funkce: .

30. 

Složenou funkci  rozepište pomocí vnější a vnitřní funkce.

Vnější funkce: , vnitřní funkce:

31. 

Složenou funkci  rozepište pomocí vnější a vnitřní funkce.

Vnější funkce: , vnitřní funkce: .