Přednášky Zadání teoretických otázek a úkolů Řešení teoretických otázek a úkolů Vzorové řešené příklady Příklady na procvičení
3 Funkce a její limita
Cíle
Na konci kapitoly bude student umět
· definovat základní typy funkcí jedné reálné proměnné,
· vyčíslit definiční obory a obory funkčních hodnot elementárních funkcí a jednoduchých funkcí z nich složených,
· načrtnout grafy elementárních funkcí,
· vyčíslit limity funkcí,
· analyzovat spojitost či nespojitost funkcí.
3.1 Funkce jedné reálné proměnné
Definice
Mějme neprázdnou podmnožinu ![]() množiny reálných čísel
množiny reálných čísel ![]() ,
, ![]() .
Reálnou funkcí jedné reálné proměnné
rozumíme zobrazení
.
Reálnou funkcí jedné reálné proměnné
rozumíme zobrazení ![]() množiny
množiny ![]() do množiny
do množiny ![]() . Tedy
. Tedy
každému ![]() jediné
jediné
![]() .
.
![]() :
: ![]()
![]() definiční
obor funkce
definiční
obor funkce ![]() , množina vzorů
, množina vzorů ![]()
![]() obor
(funkčních) hodnot funkce
obor
(funkčních) hodnot funkce ![]() , množina
obrazů
, množina
obrazů ![]()
Zápis: ![]()
![]() :
nezávisle proměnná (argument)
:
nezávisle proměnná (argument)
![]() : závisle
proměnná
: závisle
proměnná
Určete definiční obory funkcí:
![]() ;
; ![]() ;
; ![]()
Dvě funkce považujeme za sobě rovné tehdy a jen tehdy, mají‑li
týž definiční obor a přiřazují‑li obě ke každému ![]() z definičního oboru totéž
z definičního oboru totéž ![]() z oboru hodnot.
z oboru hodnot.
Grafem funkce
![]() rozumíme množinu všech bodů
rozumíme množinu všech bodů ![]() .
.
Funkce ![]() je na množině
je na množině ![]()
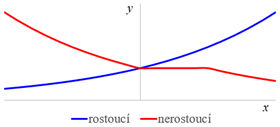
rostoucí
![]()
nerostoucí
![]()
klesající
![]()
neklesající
![]()
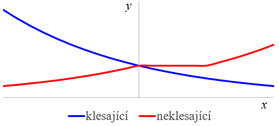
Monotónní funkce: rostoucí, nerostoucí, klesající, neklesající.
Ryze monotónní funkce: rostoucí, klesající
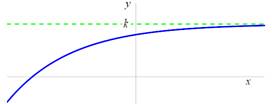
Funkce ![]() je shora
omezená (ohraničená) číslem k na množině M
je shora
omezená (ohraničená) číslem k na množině M ![]() .
.
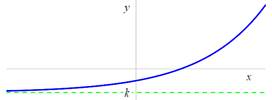
Funkce ![]() je zdola
omezená (ohraničená) číslem k na množině M
je zdola
omezená (ohraničená) číslem k na množině M ![]() .
.
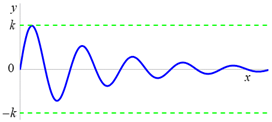
Funkce ![]() je omezená (ohraničená) na množině
je omezená (ohraničená) na množině ![]()
![]() .
.
Omezená funkce ![]() je
omezená shora číslem k a
zároveň je omezená zdola číslem
je
omezená shora číslem k a
zároveň je omezená zdola číslem ![]() .
.
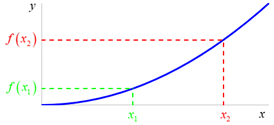
Funkce ![]() je prostá
na množině
je prostá
na množině ![]()
![]()
Funkce ![]() přiřazuje
každému
přiřazuje
každému ![]() jediné
jediné ![]() . Je-li funkce
. Je-li funkce ![]() prostá, pak také ke každému
prostá, pak také ke každému ![]() přísluší jediné
přísluší jediné ![]() . Na množině
. Na množině ![]() je definována inverzní funkce
je definována inverzní funkce ![]() k funkci
k funkci ![]() . Platí:
. Platí: ![]() ,
, ![]() ,
, ![]() .
.
Sestavení
inverzní funkce: z funkce ![]() vyjádříme
proměnnou
vyjádříme
proměnnou ![]() jako funkci proměnné
jako funkci proměnné ![]() , tj.
, tj. ![]() a
provedeme formální záměnu označení proměnných
a
provedeme formální záměnu označení proměnných ![]() .
.
Grafy vzájemně
inverzních funkcí ![]() a
a ![]() jsou vzájemně souměrné podle osy prvého a třetího kvadrantu.
jsou vzájemně souměrné podle osy prvého a třetího kvadrantu.
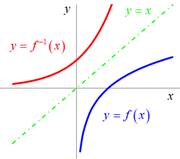
Sestavte inverzní funkci k funkci ![]() .
.
Funkce ![]() je
sudá na množině
je
sudá na množině ![]()
![]()
Graf sudé funkce je souměrný podle osy y.
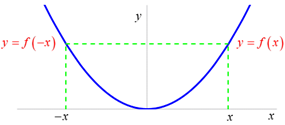
Funkce ![]() je lichá
na množině
je lichá
na množině ![]()
![]()
Graf liché funkce je souměrný podle počátku souřadného systému.
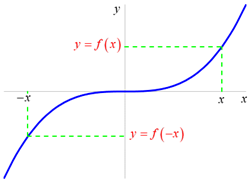
Funkce ![]() je periodická
na množině
je periodická
na množině ![]() s periodou
s periodou ![]()
![]()
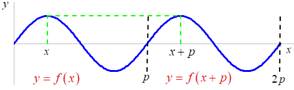
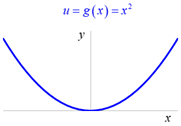
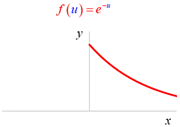
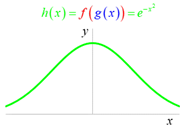
Funkce ![]() je složená
na množině
je složená
na množině ![]()
![]() ,
, ![]() ,
přičemž
,
přičemž ![]() . Kde funkce
. Kde funkce ![]() je vnější,
funkce
je vnější,
funkce ![]() je vnitřní.
je vnitřní.
|
|
|
|
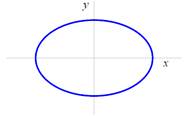
Implicitně zadaná funkce ![]()
|
|
|
|
|
Implicitně zadaná funkce |
Explicitně zadané funkce |
|
|
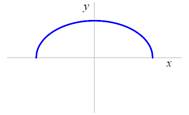
Elipsa |
Horní oblouk elipsy |
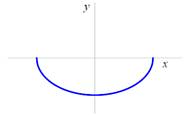
Dolní oblouk elipsy |
Příklad z praxe
 Stav
nabití
Stav
nabití ![]() autobaterie
v závislosti na hustotě
autobaterie
v závislosti na hustotě ![]() elektrolytu
lze přibližně popsat rovnicí
elektrolytu
lze přibližně popsat rovnicí ![]() .
.
Vypočítejte stav nabití autobaterie, jestliže
hustota elektrolytu ![]() .
Jaká bude hustota elektrolytu v okamžiku, kdy autobaterie bude plně
nabitá?
.
Jaká bude hustota elektrolytu v okamžiku, kdy autobaterie bude plně
nabitá?