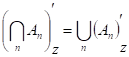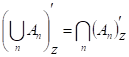Přednášky        Zadání teoretických otázek a úkolů Řešení teoretických otázek a úkolů

1.2 Množina a podmnožina

Množina

Každý úplně určený soubor objektů

Zadání množiny

• úplným seznamem prvků množiny,
• pravidlem, podle kterého lze jednoznačně rozhodnout, zda daný objekt patří, či nepatří do množiny.

 je prvkem množiny

 není prvkem množiny

         množina všech prvků , které mají vlastnost

Prázdná množina            neobsahuje žádný prvek

Konečná množina                obsahuje konečný počet prvků

Nekonečná množina             není konečná

Pozn.: Prázdné množiny řadíme mezi konečné množiny.

Množina A je podmnožinou množiny B

Rovnost dvou množin

Operace s množinami

Název operace	Označení	Definice	Vennovy diagramy
sjednocení množin A, B
průnik množin A, B
rozdíl množin A, B	;
doplněk množiny B v množině A
kartézský součin množin A, B

Množiny ,  jsou disjunktní, právě když .

Mezi podmnožinami  dané množiny  platí vztahy:

1.		komutativní zákon
2.		asociativní zákon
3.		distributivní zákon
4.
5.	, kde
6.
7.	, kde
8.	, kde
9.	,  kde po zobecnění platí:	de Morganovy vzorce