Přednášky        Zadání teoretických otázek a úkolů Řešení teoretických otázek a úkolů Vzorové řešené příklady Příklady na procvičení

1

2

2.1

2.2

2.3

2.4

2.5

2.6

2.7

2.8

2.9

2.10

2.11

2.12

2.13

2.14

2.15

2.16 Vázané extrémy

Nechť funkce  je definována na množině . Nechť  je množina bodů vyhovujících rovnici .

Potom vázanými lokálními extrémy nazýváme lokální extrémy parciální funkce, která je určena funkcí  na množině . Množinu  určuje podmínka , kterou nazýváme vazba.

a) Vazbu lze převést na explicitní vyjádření

Můžeme-li vazbu vyjádřit explicitně ve tvaru , potom funkce  je na množině  složenou funkcí jedné proměnné

a hledáme tedy extrém funkce jedné proměnné.

Příklad

Určete vázané extrémy funkce  s vazbou .

b) Vazbu nelze vyjádřit explicitně

Nechť funkce  a  patří do třídy . Zavedeme si funkci

,

kde  (nazývané Lagrangeův multiplikátor) je libovolně zvolené reálné číslo.

Jestliže má funkce  v bodu  lokální extrém, pak má v tomto bodu na množině  lokální extrém i funkce , a to extrém téhož druhu jako funkce .

Jelikož nás zajímají jen stacionární body z množiny , najdeme je řešením soustavy tří rovnic o třech neznámých :

,

,

.

O lokálním extrému ve vypočtených stacionárních bodech pak rozhodneme pomocí druhých parciálních derivací.

Příklad

Určete vázané extrémy funkce  s vazbou .

Poznámka. Metoda Lagrangeových koeficientů

Nechť funkce  je definována na množině . Nechť  je množina bodů vyhovujících vazbám

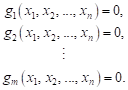
Pak si zavedeme funkci

 a dále postupujeme jako u funkce dvou proměnných.

Poznámka

Absolutní extrémy funkce  na uzavřené množině  určíme takto:

1. najdeme lokální extrémy funkce  uvnitř množiny ,

2. najdeme vázané extrémy funkce  na hranici množiny  (hranice je vazbou),

3. vybereme největší a nejmenší hodnotu z vypočtených extrémních hodnot.

Příklad

Určete absolutní extrémy funkce  na množině .