Přednášky        Zadání teoretických otázek a úkolů Řešení teoretických otázek a úkolů Vzorové řešené příklady Příklady na procvičení

1

2

2.1

2.2

2.3

2.4

2.5

2.6

2.7

2.8

2.9

2.10

2.11

2.12

2.13

2.13.1

2.13.2 Implicitně zadaná funkce dvou proměnných

Definice

Funkce  splňující rovnici  pro  nazýváme funkcí implicitně zadanou rovnicí .

Poznámka

Je-li  zadáno již jako funkce proměnných  a , pak tuto funkci nazýváme funkcí explicitně zadanou rovnicí .

Věta

Nechť

1.  je okolí bodu ,

2. , kde  je přirozené číslo,

3. , .

Pak existuje číslo  a jediná funkce  tak, že  a pro každé  je .

Výpočet prvních derivací  a  funkce  určené implicitně rovnicí . 

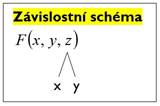
Derivujeme obě strany rovnice  s využitím pravidel pro derivování složené funkce.

Derivace podle proměnné :

,

odtud 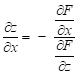,     kde .

Derivace podle proměnné :

,

odtud 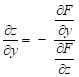,     kde .

Výpočet druhých derivací  funkce  určené implicitně rovnicí .

Nechť . Pak druhé derivace lze vypočítat opakovaným derivováním rovnice  podle jednotlivých proměnných.

Derivace druhého řádu: dvakrát derivováno podle :

první derivování podle

,

druhé derivování podle

,

odtud druhá derivace podle

.

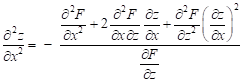Smíšená derivace druhého řádu: derivováno nejprve podle , potom podle :

první derivování podle

,

druhé derivování podle

,

odtud smíšená druhá derivace podle ,

.

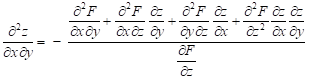Smíšená derivace druhého řádu: derivováno nejprve podle , potom podle :

první derivování podle

,

druhé derivování podle

,

odtud smíšená druhá derivace podle ,

.

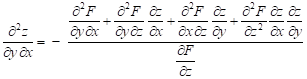Derivace druhého řádu: dvakrát derivováno podle :

první derivování podle

,

druhé derivování podle

,

odtud druhá derivace podle

.

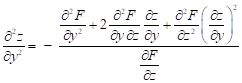Poznámka

Zcela analogicky lze postupovat při výpočtu derivací libovolných řádů implicitně zadaných funkcí více než dvou proměnných.

Příklad

Vypočítejte parciální derivace prvého řádu  a  funkce  implicitně zadané rovnicí .

Příklad

Vypočítejte parciální derivaci druhého řádu  funkce  implicitně zadané rovnicí .

Příklad

Sestavte rovnici tečné roviny ke grafu funkce  v bodu .