Přednášky        Zadání teoretických otázek a úkolů Řešení teoretických otázek a úkolů Vzorové řešené příklady Příklady na procvičení

1

2

2.1

2.2

2.3

2.4

2.5

2.6

2.7 Geometrický význam parciálních derivací

Parciální derivace  v bodu  je směrnicí tečny v bodu  ke křivce , která vznikla řezem plochy  rovinou . Tečna svírá s rovinou  úhel , pro který platí:

.

Parciální derivace  v bodu  je směrnicí tečny v bodu  ke křivce , která vznikla řezem plochy  rovinou . Tečna svírá s rovinou  úhel , pro který platí:

.

Tečná rovina v bodu  k ploše .

Rovnice tečné roviny vyplývá z podmínky komplanárnosti tří vektorů

,

kde , , .

Po dosazení do podmínky komplanárnosti tří vektorů platí:

.

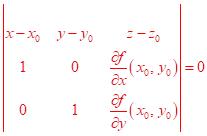Rovnice tečné roviny v bodu  k ploše :

.

Příklad

Sestavte rovnici tečné roviny ke grafu funkce  v bodu .

Příklad

Sestavte rovnici tečné roviny ke grafu funkce  tak, aby byla rovnoběžná s rovinou .