Přednášky Zadání teoretických otázek a úkolů Řešení teoretických otázek a úkolů Vzorové řešené příklady Příklady na procvičení
5.5.3 Objem rotačního tělesa
Kolem
osy ![]() rotuje
rovinný obrazec ohraničený osou x, přímkami
rotuje
rovinný obrazec ohraničený osou x, přímkami
![]() ,
, ![]() ,
,
![]() a
grafem funkce
a
grafem funkce ![]() , kde
, kde ![]() ,
, ![]() na
intervalu
na
intervalu![]() . Vzniká plné rotační těleso o objemu
. Vzniká plné rotační těleso o objemu ![]() .
.
![]()
Diferenciál
objemu pro rotaci kolem
osy ![]() :
: ![]()
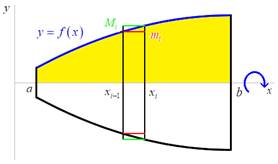
Kolem osy ![]() rotuje rovinný obrazec ohraničený
přímkami
rotuje rovinný obrazec ohraničený
přímkami ![]() ,
, ![]() ,
, ![]() a
grafy funkcí
a
grafy funkcí ![]() ,
, ![]() , kde
, kde ![]() ,
,
![]() na intervalu
na intervalu ![]() . Vzniká duté rotační těleso o objemu
. Vzniká duté rotační těleso o objemu ![]() .
.
![]()

Kolem
osy ![]() rotuje
rovinný obrazec ohraničený osou
rotuje
rovinný obrazec ohraničený osou ![]() , přímkami
, přímkami
![]() ,
, ![]() ,
,
![]() a
grafem funkce
a
grafem funkce ![]() , kde
, kde ![]() ,
, ![]() na
intervalu
na
intervalu![]() . Vzniká plné rotační těleso o objemu
. Vzniká plné rotační těleso o objemu ![]() .
.
![]()
Diferenciál
objemu pro rotaci kolem osy ![]() :
: ![]()
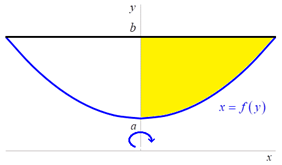
Kolem osy ![]() rotuje rovinný obrazec ohraničený
přímkami
rotuje rovinný obrazec ohraničený
přímkami ![]() ,
, ![]() ,
, ![]() a
grafy funkcí
a
grafy funkcí ![]() ,
, ![]() kde
kde ![]() ,
,
![]() na intervalu
na intervalu![]() . Vzniká duté rotační těleso o objemu
. Vzniká duté rotační těleso o objemu ![]() .
.
![]()
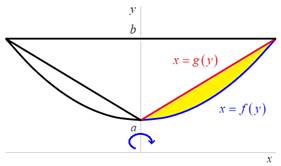
Kolem
osy ![]() rotuje rovinný obrazec
ohraničený osou
rotuje rovinný obrazec
ohraničený osou ![]() , přímkami
, přímkami ![]() ,
, ![]() a
křivkou zadanou parametrickými rovnicemi
a
křivkou zadanou parametrickými rovnicemi
![]() ,
, ![]() ,
,
![]() , kde
, kde ![]() ,
,
![]() ,
, ![]() na
intervalu
na
intervalu ![]() . Vzniká plné rotační těleso o objemu
. Vzniká plné rotační těleso o objemu ![]() .
.
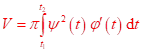
Diferenciál
objemu: ![]()
Vypočítejte objem rotačního tělesa, které vznikne rotací
kolem osy ![]() rovinného obrazce
s hranicemi:
rovinného obrazce
s hranicemi: ![]() ,
, ![]() . Řez rotačního tělesa načrtněte.
. Řez rotačního tělesa načrtněte.